/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki (OKE Poznań)
poziom rozszerzony 4 stycznia 2013 Czas pracy: 180 minut
Wyznacz resztę z dzielenia wielomianu 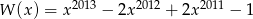 przez wielomian
przez wielomian 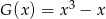 .
.
Rozwiąż równanie 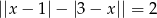 .
.
Oblicz współrzędne środka 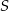 i skalę
i skalę 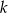 jednokładności, w której obrazem odcinka
jednokładności, w której obrazem odcinka 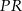 jest odcinek
jest odcinek 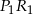 i wiadomo, że
i wiadomo, że 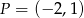 ,
, 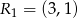 ,
, ![−→ SP 1 = [3,9 ]](https://img.zadania.info/zes/0081348/HzesT9x.gif) i
i ![−→ SR = [2,1]](https://img.zadania.info/zes/0081348/HzesT10x.gif) .
.
Długość boku rombu 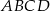 jest średnią geometryczną długości jego przekątnych. Oblicz miarę kąta ostrego tego rombu.
jest średnią geometryczną długości jego przekątnych. Oblicz miarę kąta ostrego tego rombu.
Udowodnij, że dla każdej liczby naturalnej  większej od 1 prawdziwa jest nierówność
większej od 1 prawdziwa jest nierówność
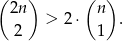
Rozwiąż równanie 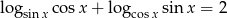 .
.
Wykaż, że pole trójkąta 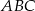 jest równe
jest równe 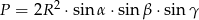 , gdzie
, gdzie 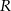 jest promieniem okręgu opisanego na tym trójkącie, a
jest promieniem okręgu opisanego na tym trójkącie, a 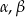 i
i 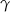 są miarami kątów wewnętrznych tego trójkąta.
są miarami kątów wewnętrznych tego trójkąta.
W ciągu arytmetycznym 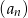 , dla
, dla 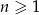 , dane są
, dane są 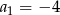 oraz różnica
oraz różnica 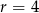 . Wyznacz największe
. Wyznacz największe  takie, że
takie, że 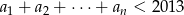 .
.
Naszkicuj wykres i wyznacz zbiór wartości funkcji określonej wzorem 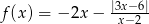 .
.
Długości wszystkich krawędzi ostrosłupa czworokątnego prawidłowego są równe  . Przez wierzchołek ostrosłupa i środki dwóch sąsiednich krawędzi podstawy poprowadzono płaszczyznę . Wyznacz sinus kąta nachylenia wyznaczonego przekroju do podstawy ostrosłupa.
. Przez wierzchołek ostrosłupa i środki dwóch sąsiednich krawędzi podstawy poprowadzono płaszczyznę . Wyznacz sinus kąta nachylenia wyznaczonego przekroju do podstawy ostrosłupa.
Do koszyka włożono 12 jabłek, w tym dwa jabłka lobo. Po kilku dniach przechowywania z koszyka usunięto dwa popsute jabłka. Następnie losowo wybrano jedno jabłko. Oblicz prawdopodobieństwo, że wybrano jabłko lobo. Wynik podaj w postaci ułamka nieskracalnego.

