/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 10 marca 2012 Czas pracy: 170 minut
Zadania zamknięte
Wskaż nierówność, którą spełnia liczba 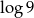 .
.
A) 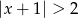 B)
B) 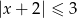 C)
C) 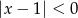 D)
D) 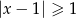
Liczba 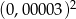 jest równa
jest równa
A) 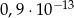 B)
B) 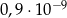 C)
C) 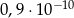 D)
D) 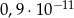
Różnica liczby  i
i 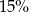 tej liczby jest równa 255. Równaniem opisującym tę zależność jest
tej liczby jest równa 255. Równaniem opisującym tę zależność jest
A) 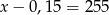 B)
B) 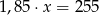 C)
C) 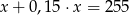 D)
D) 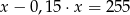
Rozwiązaniem równania 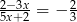 jest
jest
A) 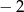 B)
B) 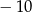 C)
C) 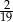 D)
D) 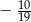
Na rysunku jest przedstawiony wykres funkcji  .
.
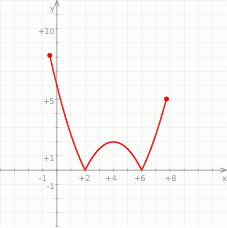
Które równanie ma dokładnie jedno rozwiązanie?
A) 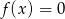 B)
B) 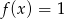 C)
C) 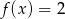 D)
D) 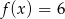
Do wykresu funkcji nie należy punkt 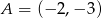 . Funkcja
. Funkcja 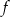 może mieć wzór
może mieć wzór
A) 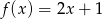 B)
B) 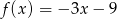 C)
C) 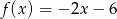 D)
D) 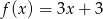
Dane są wielomiany 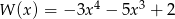 oraz
oraz 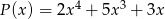 . Wielomian
. Wielomian 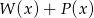 jest równy
jest równy
A) 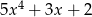
B) 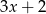
C) 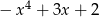
D) 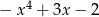
Wyrażenie 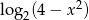 jest określone dla wszystkich liczb
jest określone dla wszystkich liczb  spełniających warunek
spełniających warunek
A) 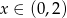 B)
B) 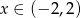 C)
C) 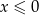 D)
D) 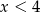
W ciągu arytmetycznym 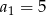 oraz
oraz 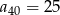 . Wtedy suma
. Wtedy suma 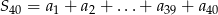 jest równa
jest równa
A) 585 B) 600 C) 1200 D) 575
Zbiorem wartości funkcji kwadratowej 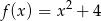 jest
jest
A) 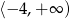 B)
B) 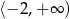 C)
C) 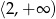 D)
D) 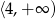
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 8 i dzieli przeciwprostokątną na dwa odcinki, z których jeden ma długość 4. Przeciwprostokątna tego trójkąta ma długość
A) 20 B) 16 C) 8 D) 18
Odcinki 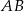 i
i 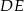 są równoległe. Długości odcinków
są równoległe. Długości odcinków 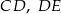 i
i 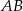 są odpowiednio równe 2, 5 i 15.
są odpowiednio równe 2, 5 i 15.
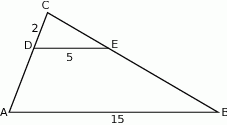
Długość odcinka 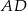 jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Pole powierzchni bocznej stożka o kącie rozwarcia 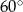 i wysokości
i wysokości 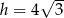 jest równe
jest równe
A) 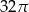 B)
B) 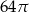 C)
C) 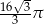 D)
D) 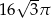
Wierzchołki trójkąta  mają współrzędne
mają współrzędne 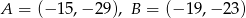 i
i 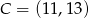 . Bok
. Bok 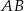 trójkąta
trójkąta 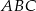 ma długość
ma długość
A) 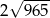 B)
B) 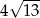 C)
C) 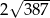 D)
D) 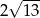
Dany jest nieskończony rosnący ciąg geometryczny 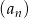 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 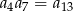 B)
B) 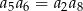 C)
C) 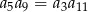 D)
D) 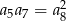
Wartość wyrażenia 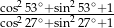 jest równa
jest równa
A) 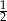 B) 0 C)
B) 0 C) 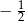 D) 1
D) 1
Ze zbioru trzycyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 30 jest równe
A) 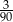 B)
B) 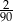 C)
C) 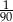 D)
D) 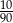
Dany jest romb o boku długości 4 i kącie ostrym 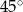 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 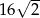 B)
B) 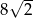 C) 16 D) 8
C) 16 D) 8
Odcinki 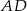 i
i 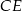 są wysokościami trójkąta
są wysokościami trójkąta 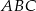 .
.
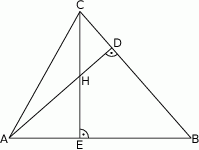
Zatem
A) 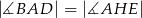
B) 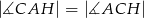
C) 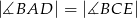
D) 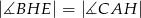
Pole powierzchni całkowitej sześcianu jest równe 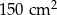 . Długość przekątnej podstawy tego sześcianu jest równa
. Długość przekątnej podstawy tego sześcianu jest równa
A) 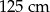 B)
B) 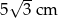 C)
C) 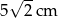 D)
D) 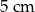
Suma miar kątów wewnętrznych wielokąta wypukłego jest równa 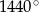 . Wynika stąd, że liczba boków tego wielokąta jest równa
. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 5 B) 7 C) 10 D) 8
Zadania otwarte
Rozwiąż równanie 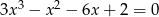 .
.
Wykaż, że nie istnieje kąt ostry  taki, że
taki, że 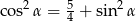 .
.
Na przeciwległych bokach równoległoboku 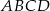 zbudowano kwadraty
zbudowano kwadraty 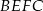 i
i 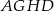 . Udowodnij, że proste
. Udowodnij, że proste 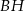 i
i 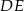 są równoległe.
są równoległe.
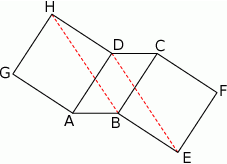
Na rysunku przedstawiono wykres funkcji 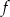 .
.
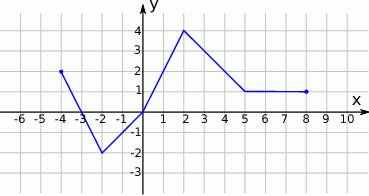
Odczytaj z wykresu i zapisz:
- zbiór wartości funkcji
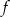 ,
, - przedział maksymalnej długości, w którym funkcja
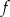 jest rosnąca.
jest rosnąca.
Wyznacz odległość między prostymi 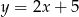 i
i 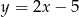 .
.
Podstawą ostrosłupa 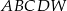 jest kwadrat
jest kwadrat 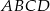 . Krawędź boczna
. Krawędź boczna  jest wysokością tego ostrosłupa. Krawędzie boczne
jest wysokością tego ostrosłupa. Krawędzie boczne 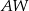 i
i 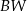 mają następujące długości:
mają następujące długości: 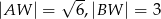 . Oblicz pole powierzchni całkowitej tego ostrosłupa.
. Oblicz pole powierzchni całkowitej tego ostrosłupa.
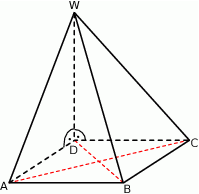
Z dwóch okrągłych kawałków blachy o średnicy 25 cm wycięto dwa prostokąty w ten sposób, że wierzchołki prostokątów znajdowały się na brzegu kół (patrz rysunek).
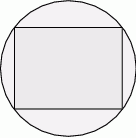
Pierwszy prostokąt miał długość o 4 cm większą niż drugi prostokąt, ale szerokość o 8 cm mniejszą. Oblicz długość i szerokość każdego z prostokątów.
W pojemniku umieszczono 50 drewnianych klocków, przy czym każdy klocek ma kształt sześcianu lub kuli, oraz każdy klocek jest czerwony lub niebieski. Wiadomo, że w pojemniku znajduje się dokładnie 15 czerwonych sześcianów, 18 klocków niebieskich i 31 klocków mających kształt kuli. Z pojemnika losowo wybieramy jeden klocek. Oblicz prawdopodobieństwo, że wylosowany klocek jest niebieską kulą.
Liczby 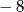 i 3 w podanej kolejności są dwoma początkowymi wyrazami ciągu arytmetycznego
i 3 w podanej kolejności są dwoma początkowymi wyrazami ciągu arytmetycznego 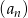 . Oblicz ile wyrazów ciągu
. Oblicz ile wyrazów ciągu 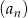 należy do przedziału
należy do przedziału 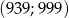 .
.

