/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 13 kwietnia 2013 Czas pracy: 180 minut
Wyznacz te wartości parametru 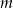 , dla których równanie
, dla których równanie
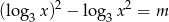
ma dwa rozwiązania należące do przedziału 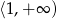 .
.
Wykaż, że jeżeli 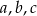 są długościami boków trójkąta to
są długościami boków trójkąta to 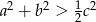 .
.
Wielomiany 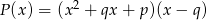 i
i 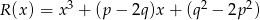 są równe. Oblicz
są równe. Oblicz 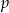 i
i 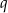 .
.
Wyznacz wszystkie liczby naturalne dodatnie 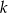 , dla których równanie
, dla których równanie 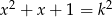 ma pierwiastki będące liczbami całkowitymi.
ma pierwiastki będące liczbami całkowitymi.
Rozwiąż równanie 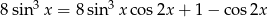 w przedziale
w przedziale 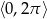 .
.
Trzy liczby o sumie 7 tworzą ciąg geometryczny. Jeżeli do drugiej liczby dodamy pierwszą to ciąg zmieni się w arytmetyczny. Wyznacz pierwszą z tych liczb. Uwzględnij wszystkie możliwości.
Do okręgów o równaniach 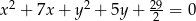 i
i 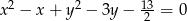 poprowadzono wspólną styczną. Oblicz długość odcinka łączącego punkty styczności. Rozważ wszystkie możliwości.
poprowadzono wspólną styczną. Oblicz długość odcinka łączącego punkty styczności. Rozważ wszystkie możliwości.
W trapezie 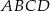 o podstawach
o podstawach 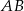 i
i 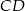 punkt
punkt 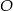 jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta
jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta 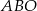 jest równe 5, a pole trójkąta
jest równe 5, a pole trójkąta 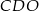 jest równe 4.
jest równe 4.
Oblicz prawdopodobieństwo 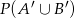 , jeśli
, jeśli 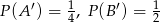 i
i 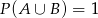 .
.
Podstawą ostrosłupa 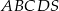 jest prostokąt o obwodzie 6. Krawędź
jest prostokąt o obwodzie 6. Krawędź 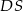 jest wysokością ostrosłupa i jest 3 razy dłuższa od krawędzi
jest wysokością ostrosłupa i jest 3 razy dłuższa od krawędzi 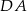 . Jakie największe pole może mieć przekrój ostrosłupa płaszczyzną wyznaczoną przez wierzchołki
. Jakie największe pole może mieć przekrój ostrosłupa płaszczyzną wyznaczoną przez wierzchołki 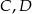 i środek krawędzi
i środek krawędzi 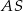 ?
?
Ile jest permutacji zbioru 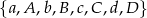 takich, w których mała litera stoi przed dużą (niekoniecznie obok) np.
takich, w których mała litera stoi przed dużą (niekoniecznie obok) np. 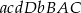 ?
?

