/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 4 maja 2019 Czas pracy: 180 minut
Zadania zamknięte
Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność 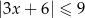 .
.
![]()
Stąd wynika, że
A) 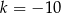 B)
B) 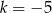 C)
C) 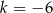 D)
D) 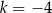
Wyrażenie 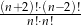 dla liczby naturalnej
dla liczby naturalnej 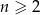 jest równe
jest równe
A) 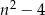 B)
B) 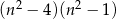 C)
C) 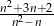 D)
D) 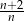
Która z poniższych funkcji nie ma minimum lokalnego ani maksimum lokalnego?
A) 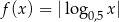 B)
B) 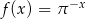 C)
C) 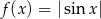 D)
D) 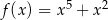
Granica 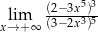 jest równa
jest równa
A) 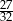 B)
B)  C)
C) 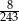 D)
D) 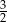
Ile jest liczb naturalnych pięciocyfrowych, których iloczyn cyfr jest dodatnią liczbą złożoną?
A) 59029 B) 59028 C) 89980 D) 89979
Zadania otwarte
Liczby 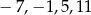 są miejscami zerowymi wielomianu czwartego stopnia
są miejscami zerowymi wielomianu czwartego stopnia 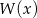 . Wykaż, że dla dowolnej liczby rzeczywistej
. Wykaż, że dla dowolnej liczby rzeczywistej  spełniona jest równość
spełniona jest równość 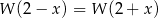 .
.
Oblicz pole trójkąta utworzonego przez prostą 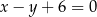 , oś
, oś 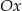 oraz styczną do wykresu funkcji
oraz styczną do wykresu funkcji 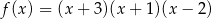 w punkcie o pierwszej współrzędnej
w punkcie o pierwszej współrzędnej 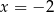 .
.
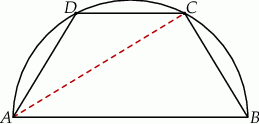
W półkole o promieniu  wpisano trapez równoramienny o przekątnej długości
wpisano trapez równoramienny o przekątnej długości 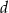 . Oblicz długość krótszej podstawy trapezu.
. Oblicz długość krótszej podstawy trapezu.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 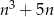 jest podzielna przez 6.
jest podzielna przez 6.
Grupę 12 uczniów, wśród których jest 6 dziewczynek i 6 chłopców podzielono na 3 równoliczne grupy. Oblicz prawdopodobieństwo tego, że w każdej z utworzonych grup będzie tyle samo dziewcząt.
Trzy parami styczne kule o promieniach równych  znajdują się w walcu w ten sposób, że każda z kul jest styczna do obu podstaw walca, oraz do jego powierzchni bocznej. Oblicz objętość walca.
znajdują się w walcu w ten sposób, że każda z kul jest styczna do obu podstaw walca, oraz do jego powierzchni bocznej. Oblicz objętość walca.
Rozwiąż równanie 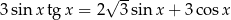 w przedziale
w przedziale 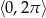 .
.
Wyznacz wszystkie wartości parametru 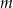 , dla których równanie
, dla których równanie 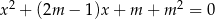 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 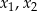 spełniające warunek:
spełniające warunek: 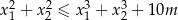 .
.
Liczby 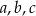 mają tę własność, że każdy z ciągów:
mają tę własność, że każdy z ciągów: 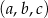 ,
, 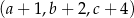 i
i 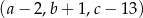 jest ciągiem geometrycznym. Oblicz
jest ciągiem geometrycznym. Oblicz 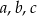 .
.
Przyprostokątna 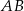 trójkąta prostokątnego
trójkąta prostokątnego 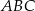 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 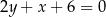 , a środek jego przeciwprostokątnej
, a środek jego przeciwprostokątnej 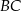 ma współrzędne
ma współrzędne 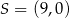 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 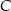 jeżeli
jeżeli 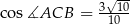 .
.
Dany jest prostokątny arkusz kartonu o długości 64 cm i szerokości 40 cm. Po dwóch stronach tego arkusza wycięto prostokąty, w których stosunek boków jest równy 1:2 (zacieniowane prostokąty na rysunku).

Następnie zagięto karton wzdłuż linii przerywanych, tworząc w ten sposób prostopadłościenne pudełko (bez przykrywki). Oblicz długości boków wyciętych prostokątów, dla których objętość otrzymanego pudełka jest największa. Oblicz tę objętość.

