/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 1 maja 2010 Czas pracy: 170 minut
Zadania zamknięte
Rozwiązaniem nierówności 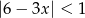 jest zbiór
jest zbiór
A) 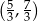 B)
B) 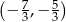 C)
C) 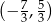 D)
D) 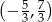
Liczba 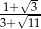 jest równa liczbie
jest równa liczbie
A) 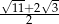 B) 9 C)
B) 9 C) 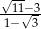 D)
D) 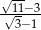
Liczba punktów wspólnych prostej 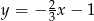 i paraboli
i paraboli 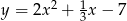 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Okręgi 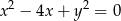 i
i 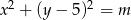 , gdzie
, gdzie 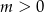 są styczne zewnętrznie. Zatem
są styczne zewnętrznie. Zatem
A) 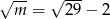 B)
B) 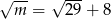 C)
C) 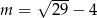 D)
D) 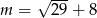
Jeżeli 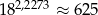 to przybliżona wartość liczby
to przybliżona wartość liczby 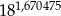 jest równa
jest równa
A) 25 B) 125 C) 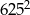 D) 3125
D) 3125
Która z podanych prostych nie przecina wykresu funkcji 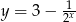 ?
?
A) 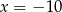 B)
B) 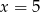 C)
C) 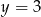 D)
D) 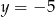
W trójkącie prostokątnym o przyprostokątnych długości 4 i 5 połączono wierzchołek 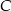 kąta prostego ze środkiem
kąta prostego ze środkiem 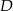 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 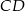 jest równa
jest równa
A) 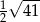 B) 4,5 C) 4 D)
B) 4,5 C) 4 D) 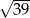
Niech 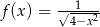 . Dziedziną funkcji
. Dziedziną funkcji 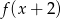 jest zbiór
jest zbiór
A) 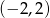 B)
B) 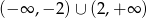 C)
C) 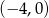 D)
D) 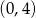
Ile rozwiązań posiada równanie 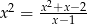 ?
?
A) 0 B) 1 C) 2 D) 3
O liczbie  wiadomo, że
wiadomo, że 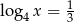 . Zatem
. Zatem
A) 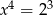 B)
B) 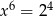 C)
C) 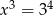 D)
D) 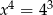
Który z podanych ciągów nie jest ciągiem geometrycznym?
A) 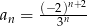 B)
B) 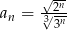 C)
C) 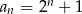 D)
D) 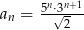
Liczba 1 jest wartością wyrażenia
A) 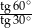 B)
B) 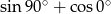 C)
C) 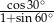 D)
D) 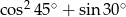
Punkt 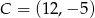 jest wierzchołkiem trójkąta równoramiennego, którego podstawa
jest wierzchołkiem trójkąta równoramiennego, którego podstawa 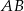 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 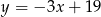 . Wysokość opuszczona na podstawę
. Wysokość opuszczona na podstawę 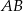 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu
A) 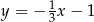 B)
B) 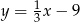 C)
C) 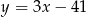 D)
D) 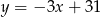
Jeden zawór napełnia basen w ciągu 55 minut, a drugi w ciągu 66 minut. W ciągu ilu minut napełnią basen oba zawory odkręcone jednocześnie?
A) 60,5 B) 40 C) 35 D) 30
Przez jaki wielomian należy pomnożyć 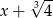 aby otrzymać wielomian
aby otrzymać wielomian 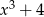 ?
?
A) 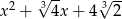
B) 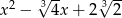
C) 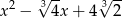
D) 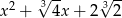
Pewne przedsiębiorstwo postanowiło przyznać każdemu pracownikowi losowy 5-cyfrowy identyfikator, przy czym ustalono, że w identyfikatorze nie może występować cyfra 0. Prawdopodobieństwo 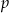 otrzymania identyfikatora, w którym każde dwie cyfry są różne spełnia warunek
otrzymania identyfikatora, w którym każde dwie cyfry są różne spełnia warunek
A) 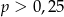 B)
B) 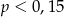 C)
C) 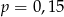 D)
D) 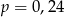
Przekątne trapezu 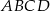 przecinają się w punkcie
przecinają się w punkcie 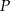 w ten sposób, że
w ten sposób, że 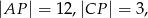
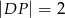 . Długość odcinka
. Długość odcinka 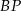 jest równa
jest równa
A) 18 B) 16 C) 9 D) 8
Samochód połowę drogi przebył ze średnią prędkością 30 km/h, a drugą połowę drogi ze średnią prędkością 60 km/h. Zatem średnia prędkość samochodu na całej trasie jest równa
A) 40 km/h B) 45 km/h C) 50 km/h D) 55 km/h
Narysowana bryła ma w podstawie kwadrat, a krawędzie boczne są prostopadłe do podstawy. Objętość tej bryły jest równa
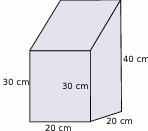
A) 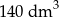 B)
B) 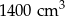 C)
C) 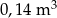 D)
D) 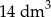
Jeżeli 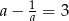 to liczba
to liczba 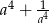 jest równa
jest równa
A) 121 B) 119 C) 123 D) 81
Zadania otwarte
Oblicz sumę liczb dwucyfrowych, które przy dzieleniu przez 8 dają resztę 2 lub 4.
Oblicz sumę długości przekątnych rombu wiedząc, że suma ich kwadratów jest równa 313, a pole rombu jest równe 78.
Rozmieniono 34 złote na 116 monet, wśród których były tylko monety 50 i 20 groszowe. Ile było monet 50 groszowych?
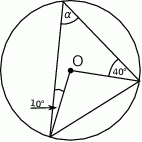
Wiedząc, że punkt 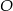 jest środkiem okręgu, oblicz miarę kąta
jest środkiem okręgu, oblicz miarę kąta  .
.
Rozwiąż równanie 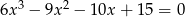 .
.
Na bokach trójkąta równobocznego zbudowano dwa kwadraty w sposób pokazany na rysunku.
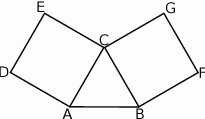
Wykaż, że punkty 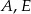 i
i 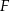 są wierzchołkami trójkąta prostokątnego.
są wierzchołkami trójkąta prostokątnego.
Na podstawie podanego wykresu funkcji 
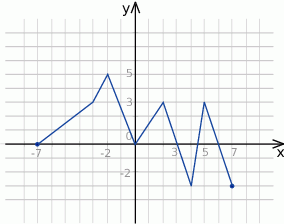
- Wyznacz zbiór wartości funkcji.
- Podaj najdłuższy przedział na którym funkcja jest rosnąca.
- Podaj liczbę rozwiązań równania
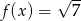 .
. - Oblicz w ilu punktach wykres funkcji
![g(x) = [f (x )]2](https://img.zadania.info/zes/0082109/HzesT93x.gif) przecina prostą
przecina prostą 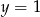 .
.
Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź podstawy ma długość 2, a krawędź boczna długość 6.
W malejącym ciągu arytmetycznym 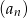 spełnione są warunki
spełnione są warunki 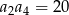 oraz
oraz 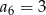 . Wyznacz sumę 10 początkowych wyrazów tego ciągu.
. Wyznacz sumę 10 początkowych wyrazów tego ciągu.

