/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki poziom rozszerzony 5 maja 2010 Czas pracy: 180 minut
Rozwiąż nierówność 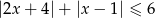 .
.
Wyznacz wszystkie rozwiązania równania 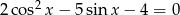 należące do przedziału
należące do przedziału 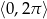 .
.
Bok kwadratu 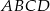 ma długość 1. Na bokach
ma długość 1. Na bokach 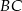 i
i 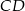 wybrano odpowiednio punkty
wybrano odpowiednio punkty 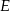 i
i 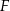 umieszczone tak, by
umieszczone tak, by 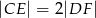 . Oblicz wartość
. Oblicz wartość 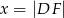 , dla której pole trójkąta
, dla której pole trójkąta 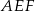 jest najmniejsze.
jest najmniejsze.
Wyznacz wartości  i
i 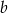 współczynników wielomianu
współczynników wielomianu 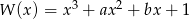 wiedząc, że
wiedząc, że 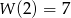 oraz, że reszta z dzielenia
oraz, że reszta z dzielenia 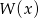 przez
przez 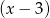 jest równa 10.
jest równa 10.
O liczbach 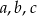 wiemy, że ciąg
wiemy, że ciąg 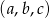 jest arytmetyczny i
jest arytmetyczny i 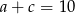 , zaś ciąg
, zaś ciąg 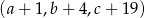 jest geometryczny. Wyznacz te liczby.
jest geometryczny. Wyznacz te liczby.
Wyznacz wszystkie wartości parametru 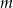 , dla których równanie
, dla których równanie 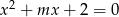 ma dwa różne pierwiastki rzeczywiste takie, że suma ich kwadratów jest większa od
ma dwa różne pierwiastki rzeczywiste takie, że suma ich kwadratów jest większa od 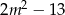 .
.
Punkt 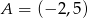 jest jednym z wierzchołków trójkąta równoramiennego
jest jednym z wierzchołków trójkąta równoramiennego 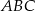 , w którym
, w którym 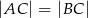 . Pole tego trójkąta jest równe 15. Bok
. Pole tego trójkąta jest równe 15. Bok 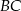 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 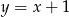 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 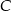 .
.
Rysunek przedstawia fragment wykresu funkcji 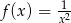 .
.
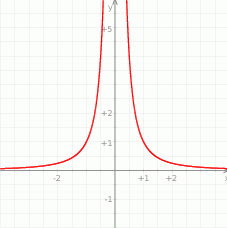
Przeprowadzono prostą równoległą do osi 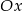 , która przecięła wykres tej funkcji w punktach
, która przecięła wykres tej funkcji w punktach 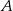 i
i 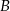 . Niech
. Niech 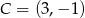 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 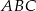 jest większe lub równe 2.
jest większe lub równe 2.
Na bokach 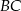 i
i 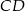 równoległoboku
równoległoboku 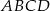 zbudowano kwadraty
zbudowano kwadraty 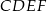 i
i 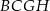 (zobacz rysunek).
(zobacz rysunek).
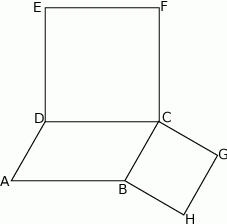
Udowodnij, że 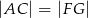 .
.
Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb uzyskanych oczek będzie podzielna przez 3.
W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość  . Ściany boczne są trójkątami ostrokątnymi. Miara kąta między sąsiednimi ścianami bocznymi jest równa
. Ściany boczne są trójkątami ostrokątnymi. Miara kąta między sąsiednimi ścianami bocznymi jest równa 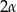 . Wyznacz objętość tego ostrosłupa.
. Wyznacz objętość tego ostrosłupa.

