/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki poziom rozszerzony 5 marca 2019 Czas pracy: 180 minut
Zadania zamknięte
Liczba miejsc zerowych funkcji 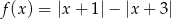 , gdzie
, gdzie 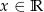 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Jeżeli 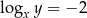 to
to 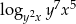 jest równy
jest równy
A) 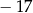 B)
B) 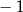 C) 3 D)
C) 3 D) 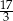
Objętość stożka o promieniu podstawy równym  jest równa
jest równa 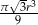 . Miara kąta rozwarcia tego stożka jest równa
. Miara kąta rozwarcia tego stożka jest równa
A) 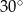 B)
B) 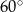 C)
C) 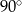 D)
D) 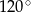
Granica ciągu 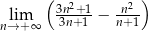 jest równa
jest równa
A) 1 B)  C)
C)  D)
D) 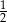
Jeżeli 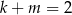 i
i 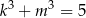 , to wartość iloczynu
, to wartość iloczynu 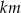 jest równa
jest równa
A)  B)
B) 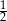 C)
C)  D)
D) 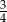
Zadania otwarte
Oblicz sumę czwartych potęg pierwiastków równania 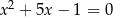 .
.
Oblicz wartość wyrażenia 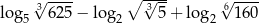 .
.
Wyznacz współrzędne punktu należącego do wykresu funkcji 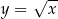 i takiego, że styczna do krzywej w tym punkcie jest nachylona do osi
i takiego, że styczna do krzywej w tym punkcie jest nachylona do osi 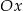 pod kątem
pod kątem 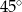 .
.
Zbadaj dla jakich wartości parametru  istnieje rozwiązanie równania
istnieje rozwiązanie równania
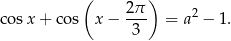
Długości boków trapezu prostokątnego tworzą ciąg geometryczny. Ramię, które jest najkrótszym bokiem trapezu ma długość 1. Krótsza podstawa trapezu jest krótsza od drugiego z ramion. Oblicz długość dłuższej podstawy.
Na ile sposobów można wybrać ze zbioru 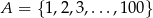 trzy różne liczby, których suma przy dzieleniu przez 3 daje resztę 1.
trzy różne liczby, których suma przy dzieleniu przez 3 daje resztę 1.
Dla jakich wartości parametru 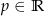 równanie
równanie 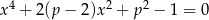 ma dokładnie dwa różne rozwiązania?
ma dokładnie dwa różne rozwiązania?
W trapezie 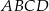 dane są długości podstaw:
dane są długości podstaw: 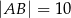 ,
, 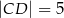 i ramion:
i ramion: 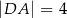 ,
, 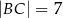 . Oblicz długość przekątnej
. Oblicz długość przekątnej 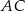 tego trapezu.
tego trapezu.
Dwie maszyny wykonują detale: pierwsza maszyna 75%, a druga 25%. Wśród detali maszyny pierwszej 95%, a maszyny drugiej 80% odpowiada wymogom technicznym. Wylosowano jeden detal, który odpowiada wymogom technicznym. Jakie jest prawdopodobieństwo, że detal ten pochodzi z maszyny drugiej?
Wyznacz równania prostych stycznych do okręgu o równaniu 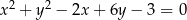 i zarazem prostopadłych do prostej
i zarazem prostopadłych do prostej 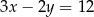 .
.
Wyznacz wszystkie wartości parametru 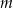 , dla których funkcja
, dla których funkcja 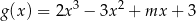 ma ekstremum lokalne równe 10.
ma ekstremum lokalne równe 10.
We wnętrzu sześcianu umieszczono czworościan foremny w ten sposób, że wszystkie krawędzie czworościanu są przekątnymi ścian bocznych sześcianu. Wyznacz stosunek objętości czworościanu do objętości sześcianu.

