/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom podstawowy 2 czerwca 2022 Czas pracy: 170 minut
Zadania zamknięte
Liczba 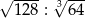 jest równa
jest równa
A) 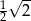 B) 2 C)
B) 2 C) 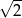 D)
D) 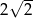
Liczba 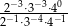 jest równa
jest równa
A) 1 B) 3 C) 24 D) 48
Liczba dwukrotnie większa od 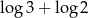 jest równa
jest równa
A) 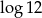 B)
B) 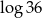 C)
C) 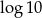 D)
D) 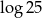
30% liczby  jest o 2730 mniejsze od liczby
jest o 2730 mniejsze od liczby  . Liczba
. Liczba  jest równa
jest równa
A) 3900 B) 1911 C) 9100 D) 2100
Dla każdej liczby rzeczywistej  wyrażenie
wyrażenie 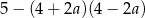 jest równe
jest równe
A) 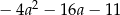 B)
B) 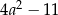 C)
C) 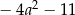 D)
D) 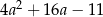
Jedną z liczb spełniających nierówność 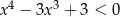 jest
jest
A) 1 B) 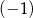 C) 2 D)
C) 2 D) 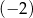
Informacja do zadań 7 i 8
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 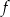 określonej wzorem
określonej wzorem 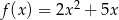 .
.
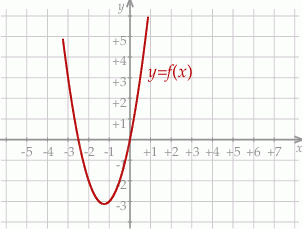
Osią symetrii wykresu funkcji 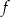 jest prosta o równaniu
jest prosta o równaniu
A) 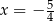 B)
B) 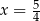 C)
C) 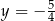 D)
D) 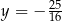
Funkcja kwadratowa 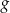 jest określona wzorem
jest określona wzorem 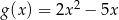 . Wykres funkcji
. Wykres funkcji 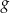 jest
jest
A) symetryczny do wykresu funkcji 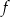 względem osi
względem osi 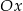 .
.
B) symetryczny do wykresu funkcji 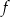 względem osi
względem osi 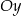 .
.
C) symetryczny do wykresu funkcji 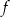 względem początku układu współrzędnych.
względem początku układu współrzędnych.
D) przesunięty względem wykresu funkcji 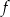 o 10 jednostek w kierunku przeciwnym do zwrotu osi
o 10 jednostek w kierunku przeciwnym do zwrotu osi 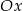 .
.
Równanie 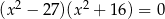 ma dokładnie
ma dokładnie
A) jedno rozwiązanie rzeczywiste.
B) dwa rozwiązania rzeczywiste.
C) trzy rozwiązania rzeczywiste.
D) cztery rozwiązania rzeczywiste.
Funkcja 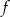 jest określona wzorem
jest określona wzorem 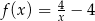 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 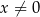 . Liczba
. Liczba 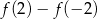 jest równa
jest równa
A) 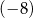 B)
B) 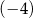 C) 4 D) 0
C) 4 D) 0
Punkt 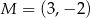 należy do wykresu funkcji liniowej
należy do wykresu funkcji liniowej 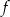 określonej wzorem
określonej wzorem
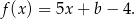
Wynika stąd, że 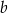 jest równe
jest równe
A) 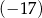 B)
B) 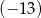 C) 13 D) 17
C) 13 D) 17
Funkcja kwadratowa 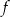 określona wzorem
określona wzorem 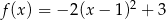 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 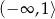 B)
B) 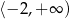 C)
C) 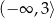 D)
D) 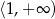
Na rysunku jest przedstawiony fragment wykresu funkcji 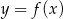 .
.
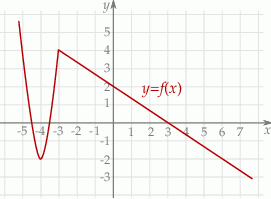
W przedziale 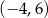 równanie
równanie 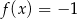
A) nie ma rozwiązań.
B) ma dokładnie dwa rozwiązania.
C) ma dokładnie trzy rozwiązania.
D) ma nieskończenie wiele rozwiązań.
Ciąg 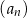 jest określony wzorem
jest określony wzorem 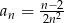 dla każdej liczby naturalnej
dla każdej liczby naturalnej 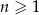 . Piąty wyraz tego ciągu jest równy
. Piąty wyraz tego ciągu jest równy
A) 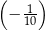 B)
B) 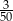 C)
C) 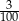 D)
D) 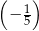
Ciąg 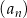 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 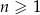 , jest arytmetyczny. Różnica tego ciągu jest równa 2 oraz
, jest arytmetyczny. Różnica tego ciągu jest równa 2 oraz 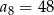 . Czwarty wyraz tego ciągu jest równy
. Czwarty wyraz tego ciągu jest równy
A) 2 B) 24 C) 3 D) 40
Kąt  jest ostry i
jest ostry i 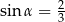 . Wtedy
. Wtedy 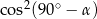 jest równy
jest równy
A) 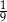 B)
B) 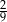 C)
C) 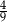 D)
D) 
Na trójkącie ostrokątnym 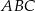 opisano okrąg o środku
opisano okrąg o środku 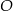 . Miara kąta
. Miara kąta 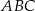 jest równa
jest równa 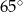 . Miara kąta
. Miara kąta 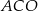 jest równa
jest równa
A) 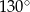 B)
B) 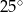 C)
C) 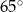 D)
D) 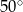
Trójkąt 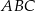 jest prostokątny. Odcinek
jest prostokątny. Odcinek 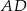 jest wysokością tego trójkąta poprowadzoną z wierzchołka
jest wysokością tego trójkąta poprowadzoną z wierzchołka 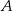 na przeciwprostokątną
na przeciwprostokątną 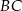 . Wtedy
. Wtedy
A) 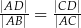 B)
B) 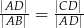 C)
C) 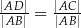 D)
D) 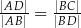
Pole rombu o obwodzie 20 i kącie rozwartym 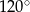 jest równe
jest równe
A) 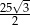 B)
B) 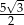 C)
C) 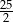 D)
D) 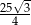
W trójkącie miary kątów są równe:  ,
, 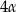 ,
, 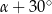 . Miara największego kąta tego trójkąta jest równa
. Miara największego kąta tego trójkąta jest równa
A) 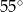 B)
B) 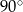 C)
C) 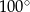 D)
D) 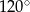
Na boku 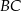 kwadratu
kwadratu 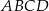 (na zewnątrz) zbudowano trójkąt równoboczny
(na zewnątrz) zbudowano trójkąt równoboczny 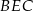 (zobacz rysunek).
(zobacz rysunek).
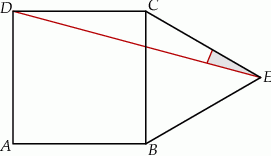
Miara kąta 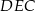 jest równa
jest równa
A) 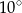 B)
B) 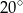 C)
C) 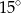 D)
D) 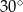
Proste o równaniach 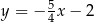 oraz
oraz 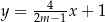 są prostopadłe. Wynika stąd, że
są prostopadłe. Wynika stąd, że
A) 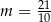 B)
B) 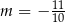 C)
C) 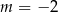 D)
D) 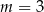
Proste o równaniach 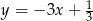 oraz
oraz 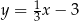 przecinają się w punkcie
przecinają się w punkcie 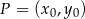 . Wynika stąd, że
. Wynika stąd, że
A) 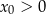 i
i 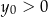 B)
B) 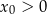 i
i 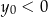 C)
C) 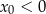 i
i 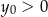 D)
D) 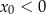 i
i 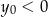
Liczba wszystkich krawędzi graniastosłupa jest równa 42. Liczba wszystkich wierzchołków tego graniastosłupa jest równa
A) 14 B) 28 C) 15 D) 42
W ostrosłupie prawidłowym trójkątnym wszystkie krawędzie mają długość 8. Pole powierzchni całkowitej tego ostrosłupa jest równe
A) 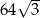 B)
B) 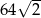 C)
C) 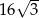 D)
D) 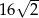
Rozważamy wszystkie liczby naturalne czterocyfrowe, których suma cyfr jest równa 3. Wszystkich takich liczb jest
A) 13 B) 10 C) 7 D) 9
W pudełku są tylko kule białe, czarne i zielone. Kul białych jest dwa razy więcej niż czarnych, a czarnych jest trzy razy więcej niż zielonych. Z pudełka losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli białej jest równe
A)  B)
B) 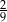 C)
C) 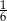 D)
D) 
W pewnej grupie uczniów przeprowadzono ankietę na temat liczby odsłuchanych audiobooków w lutym 2022 roku. Wyniki ankiety przedstawiono w tabeli.
| Liczba odsłuchanych audiobooków | 0 | 1 | 2 | 3 | 4 | 7 |
| Liczba uczniów | 9 | 5 | 3 | 4 | 1 | 3 |
Mediana liczby odsłuchanych audiobooków w tej grupie uczniów jest równa
A) 3 B) 2 C) 1 D) 
Zadania otwarte
Rozwiąż nierówność 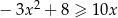 .
.
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 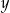 takich, że
takich, że 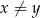 prawdziwa jest nierówność
prawdziwa jest nierówność
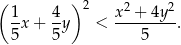
Funkcja kwadratowa 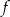 ma dokładnie jedno miejsce zerowe równe 2. Ponadto
ma dokładnie jedno miejsce zerowe równe 2. Ponadto 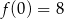 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 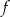 .
.
Trójwyrazowy ciąg 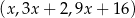 jest geometryczny. Oblicz
jest geometryczny. Oblicz  .
.
Dany jest trapez prostokątny 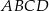 . Podstawa
. Podstawa 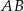 tego trapezu jest równa 26, a ramię
tego trapezu jest równa 26, a ramię 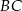 ma długość 24. Przekątna
ma długość 24. Przekątna 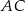 tego trapezu jest prostopadła do ramienia
tego trapezu jest prostopadła do ramienia 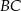 (zobacz rysunek).
(zobacz rysunek).
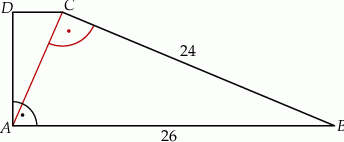
Oblicz długość ramienia 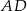 .
.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych większych od 53 losujemy jedną liczbę. Niech 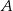 oznacza zdarzenie polegające na wylosowaniu liczby podzielnej przez 7. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na wylosowaniu liczby podzielnej przez 7. Oblicz prawdopodobieństwo zdarzenia 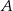 .
.
Punkt 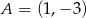 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 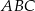 , w którym
, w którym 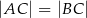 . Punkt
. Punkt 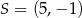 jest środkiem odcinka
jest środkiem odcinka 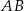 . Wierzchołek
. Wierzchołek 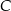 tego trójkąta leży na prostej o równaniu
tego trójkąta leży na prostej o równaniu 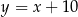 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 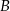 i
i 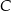 tego trójkąta.
tego trójkąta.

