/Szkoła średnia/Zadania maturalne
Poprawkowy Egzamin Maturalny
z Matematyki poziom rozszerzony 23 sierpnia 2010 Czas pracy: 180 minut
Wyznacz wszystkie rozwiązania równania 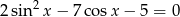 należące do przedziału
należące do przedziału 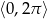 .
.
Rozwiąż nierówność 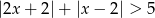 .
.
Dane są punkty 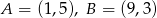 i prosta
i prosta 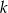 o równaniu
o równaniu 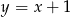 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 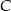 leżącego na prostej
leżącego na prostej 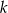 , dla którego suma
, dla którego suma 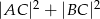 jest najmniejsza.
jest najmniejsza.
Wyznacz wszystkie wartości parametru 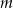 , dla których równanie
, dla których równanie 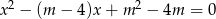 ma dwa różne pierwiastki rzeczywiste, których suma jest mniejsza od
ma dwa różne pierwiastki rzeczywiste, których suma jest mniejsza od 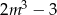 .
.
Narysuj wykres funkcji 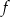 określonej wzorem
określonej wzorem 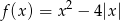 i na jego podstawie wyznacz liczbę rozwiązań równania
i na jego podstawie wyznacz liczbę rozwiązań równania 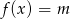 w zależności od wartości parametru
w zależności od wartości parametru 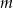 .
.
Wykaż, że dla dowolnych liczb rzeczywistych 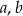 spełniona jest nierówność
spełniona jest nierówność
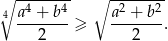
Objętość graniastosłupa prawidłowego trójkątnego jest równa 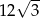 , a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.
, a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.
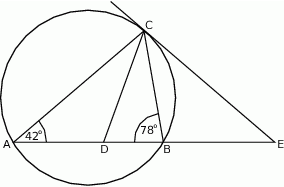
Odcinek 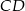 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 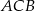 trójkąta
trójkąta 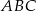 . Kąty trójkąta
. Kąty trójkąta 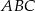 mają miary
mają miary 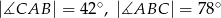 . Styczna do okręgu opisanego na tym trójkącie w punkcie
. Styczna do okręgu opisanego na tym trójkącie w punkcie 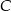 przecina prostą
przecina prostą 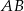 w punkcie
w punkcie 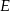 (zobacz rysunek). Oblicz, ile stopni ma każdy z kątów trójkąta
(zobacz rysunek). Oblicz, ile stopni ma każdy z kątów trójkąta 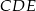 .
.
Liczby 1, 2, 3, 4, 5, 6, 7, 8 ustawiamy losowo w szeregu. Oblicz prawdopodobieństwo, że w tym ustawieniu suma każdych dwóch sąsiednich liczb będzie nieparzysta. Wynik podaj w postaci ułamka nieskracalnego.
Punkt 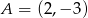 jest wierzchołkiem rombu
jest wierzchołkiem rombu 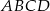 o polu równym 300. Punkt
o polu równym 300. Punkt 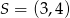 jest środkiem symetrii tego rombu. Wyznacz współrzędne pozostałych wierzchołków tego rombu.
jest środkiem symetrii tego rombu. Wyznacz współrzędne pozostałych wierzchołków tego rombu.
Ciąg 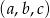 jest geometryczny i
jest geometryczny i 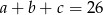 , zaś ciąg
, zaś ciąg 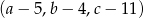 jest arytmetyczny. Oblicz
jest arytmetyczny. Oblicz 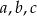 .
.

