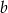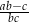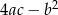Zadania.info: zestaw nr. 82741, Próbna matura 2008, poziom podstawowy (OKE Poznań),5

Podobne strony

Próbny Egzamin Maturalny
z Matematyki (OKE Poznań)
poziom podstawowy styczeń 2008 Czas pracy: 120 minut

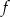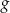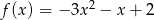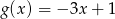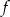Zadanie 1 (3 pkt.)Funkcje $f$ i $g$ dane są wzorami $f(x) = − 3x 2 − x + 2$ , $g(x) = −3x + 1$ . Wyznacz zbiór argumentów $x$ , dla których funkcja $f$ przyjmuje wartości większe od funkcji $g$ .

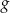Zadanie 2 (5 pkt.)Obroty pewnej ﬁrmy w pierwszych trzech kwartałach 2007 roku utworzyły ciąg geometryczny, a w ciągu ostatnich trzech kwartałów ciąg arytmetyczny. W drugim kwartale obroty ﬁrmy wynosiły 15 000zł, a w czwartym 22 500zł. Oblicz średnie miesięczne obroty ﬁrmy.

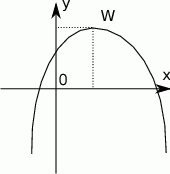
Zadanie 3 (4 pkt.)Wyznacz dziedzinę funkcji 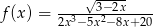$√ ----- f(x) = --3--3−22x---- 2x− 5x− 8x+20$ .

Zadanie 4 (5 pkt.)Wierzchołek kąta znajduje się w punkcie 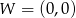$W = (0,0)$ , jedno z jego ramion leży na prostej 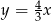$y = 43x$ , a drugie ramię przechodzi przez punkt 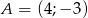$A = (4;− 3)$ . Punkt 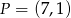$P = (7,1)$ należy do wnętrza tego kąta. Sprawdź rachunkowo, czy punkt 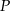$P$ leży na dwusiecznej tego kąta.

Zadanie 5 (5 pkt.)Wykorzystując poniższy szkic wykresu funkcji kwadratowej o równaniu 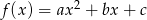$f(x) = ax 2 + bx+ c$ , gdzie 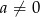$a ⁄= 0$ określ znak następujących wyrażeń:

$a$
$b$
$c$
$ab−c bc$
$4ac − b2$

Zadanie 6 (5 pkt.)Co czwarta kula w urnie to biała, pozostałe mają kolor czarny lub niebieski. Losujemy jedna kulę. Prawdopodobieństwo wylosowania kuli niebieskiej lub białej jest dwukrotnie mniejsze niż prawdopodobieństwo wylosowania kuli niebieskiej lub czarnej. Oblicz prawdopodobieństwo wylosowania kuli czarnej.

Zadanie 7 (3 pkt.)Rozwiąż równanie 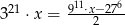$21 911⋅x− 276 3 ⋅x = ----2---$ .

Zadanie 8 (5 pkt.)Obserwator stojący na płaskiej, poziomej powierzchni widzi pionową wieżę pod kątem 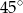$45∘$ , a po zbliżeniu się do niej o 20m pod kątem 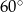$60∘$ . Oblicz wysokość wieży, wynik zaokrąglij do 1cm.

Zadanie 9 (4 pkt.)W wyniku tzw. złotego podziału odcinka otrzymuje się dwa nowe odcinki o tej własności, że stosunek krótszego z nich do dłuższego jest równy stosunkowi dłuższego z nich do całego odcinka. Dokonano złotego podziału odcinka o długości 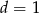$d = 1$ , oblicz długość krótszej części.

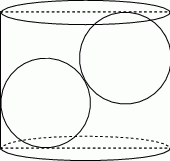
Zadanie 10 (6 pkt.)W pojemniku o kształcie walca o promieniu podstawy 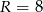$R = 8$ umieszczono dwie kule o promieniu 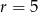$r = 5$ , w ten sposób, że są do siebie styczne i każda z nich dotyka powierzchni bocznej walca, jak na rysunku. Jaka co najmniej musi być wysokość pojemnika, aby kule całkowicie się w nim mieściły. Oblicz objętość tego walca.

Zadanie 11 (5 pkt.)Różnica kwadratów długości przekątnych trapezu prostokątnego wynosi 21, jego wysokość ma długość 4, a dłuższe ramię ma długość 5. Oblicz pole trapezu.

Rozwiązania

Wersja PDF

Szybka nauka - praktyczne ćwiczenia	Angielskie formuły konwersacyjne i Angielskie przyimki

19,97 zł 93 specjalne ćwiczenia, dzięki którym nauka nie będzie sprawiać Ci problemów.	15,90 zł Poznaj komplet angielskich przyimków oraz formuł konwersacyjnych.