/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 26 kwietnia 2008 Czas pracy: 120 minut

Zadanie 1
(5 pkt)

Na podstawie podanego wykresu funkcji f

PIC

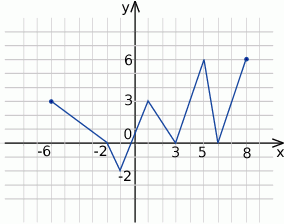
  • wyznacz największą i najmniejszą wartość funkcji;
  • podaj najdłuższy przedział na którym funkcja jest malejąca;
  • zapisz w postaci sumy przedziałów zbiór rozwiązań nierówności f(x) < 3 ;
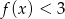  • oblicz w ilu punktach wykres funkcji g(x) = [f(x )]2 przecina prostą y = 4 .

Zadanie 2
(4 pkt)

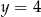W sześcianie o krawędzi długości 2 połączono ze sobą środki trzech ścian mających wspólny wierzchołek. Sporządź odpowiedni rysunek i oblicz pole otrzymanego trójkąta.

Zadanie 3
(5 pkt)

Sprzedawca kwiatów notował w tabeli ilość otrzymanych banknotów z podziałem według ich nominałów.

  1 dzień 2 dzień 3 dzień 4 dzień 5 dzień
10 zł 2 7 4 6 1
20 zł 5 5 2 4 3
50 zł 2 3 0 3 5
100 zł 1 3 1 1 2
  • Podaj, w których dniach jego przychody były wyższe niż średni dzienny przychód w ciągu tych pięciu dni.
  • Oblicz odchylenie standardowe liczby otrzymanych banknotów w ciągu tych pięciu dni. Wynik podaj z dokładnością do 0,1.

Zadanie 4
(5 pkt)

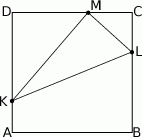
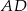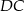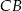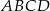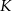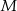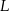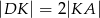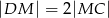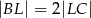Na bokach AD , DC i CB kwadratu ABCD wybrano punkty K , M i L ten sposób, że |DK | = 2 |KA | , |DM | = 2|MC | , oraz |BL | = 2|LC | .

  • Uzasadnij, że trójkąt 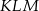KLM jest prostokątny.
  • Oblicz tangensy kątów ostrych trójkąta KLM .
PIC

Zadanie 5
(6 pkt)

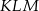Wykres funkcji kwadratowej 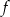f jest styczny do prostej 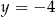y = − 4 , przechodzi przez punkt 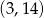(3,14 ) oraz jest symetryczny względem osi Oy .

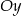  • Wyznacz wzór funkcji 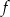f i narysuj jej wykres.
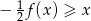
  • Rozwiąż nierówność 1 − 2f(x) ≥ x

Zadanie 6
(3 pkt)

Janek, Tomek i Łukasz zbierali pieniądze na zakup piłki. Janek dał 60% potrzebnej kwoty, Tomek dał 40% pozostałej części. Łukasz dołożył brakujące 48 zł. Ile kosztowała piłka?

Zadanie 7
(5 pkt)

Dany jest okrąg o środku w punkcie 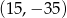(1 5,− 35) i promieniu 16. Sprawdź czy okrąg ten jest styczny do

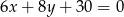  • prostej 6x + 8y + 30 = 0 ,
  • okręgu o środku w punkcie 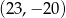(2 3,− 20) i promieniu 2?

Uzasadnij swoją odpowiedź.

Zadanie 8
(5 pkt)

Wszystkie liczby parzyste z przedziału 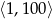⟨1 ,1 00⟩ , które nie są podzielne przez 4 ustawiamy w ciąg (an) .

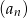  • Wyznacz wzór ciągu 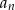an i uzasadnij, że jest on arytmetyczny.
  • Oblicz sumę wszystkich wyrazów tego ciągu.

Zadanie 9
(5 pkt)

Wiedząc, że wielomian 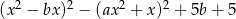(x2 − bx )2 − (ax 2 + x )2 + 5b + 5 jest wielomianem stopnia 3 oraz 1 jest jego pierwiastkiem wyznacz a i b .

Zadanie 10
(4 pkt)

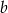Spośród 5 monet jednozłotowych, 7 dwuzłotowych i 6 pięciozłotowych wybieramy 3 monety. Oblicz prawdopodobieństwo, że wszystkie trzy monety będą miały ten sam nominał.

Zadanie 11
(3 pkt)

Suma pól dwóch kół stycznych zewnętrznie jest równa 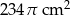234π cm 2 . Oblicz promienie tych kół, jeżeli wiadomo, że obwód większego koła jest o 400% większy od obwodu mniejszego koła.

Arkusz Wersja PDF
Rozwiązania