/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki (CKE)
poziom rozszerzony 4 marca 2022 Czas pracy: 180 minut
Dane są liczby 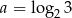 oraz
oraz 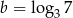 . Wyraź
. Wyraź 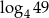 za pomocą
za pomocą  oraz
oraz 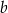 .
.
Funkcja 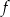 jest określona wzorem
jest określona wzorem 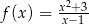 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 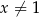 . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie 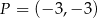 .
.
Dany jest nieskończony ciąg geometryczny 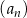 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 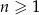 . Suma trzech początkowych wyrazów ciągu
. Suma trzech początkowych wyrazów ciągu 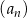 jest równa 7, a suma
jest równa 7, a suma 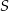 wszystkich wyrazów tego ciągu jest równa 8. Wyznacz wszystkie wartości
wszystkich wyrazów tego ciągu jest równa 8. Wyznacz wszystkie wartości  , dla których spełniona jest nierówność
, dla których spełniona jest nierówność
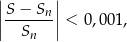
gdzie 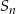 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 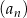 .
.
Dane jest równanie
![2 (x − 6) ⋅[(m − 2)x − 4(m + 3)x + m + 1] = 0](https://img.zadania.info/zes/0083221/HzesT18x.gif)
z niewiadomą  i parametrem
i parametrem 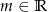 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 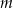 , dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
, dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
Udowodnij, że suma sześcianów trzech kolejnych liczb całkowitych niepodzielnych przez 4 jest liczbą podzielną przez 36.
Informacja do zadań 6.1 i 6.2
Na obrzeżach miasta znajduje się jezioro, na którym postanowiono stworzyć tor regatowy. Na podstawie dostępnych map wymodelowano w pewnej skali kształt linii brzegowej jeziora w kartezjańskim układzie współrzędnych 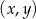 za pomocą fragmentów wykresów funkcji
za pomocą fragmentów wykresów funkcji 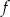 oraz
oraz 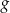 (zobacz rysunek).
(zobacz rysunek).
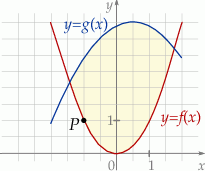
Funkcje 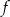 oraz
oraz 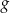 są określone wzorami
są określone wzorami 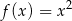 oraz
oraz 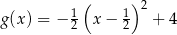 . Początek toru postanowiono zlokalizować na brzegu jeziora w miejscu, któremu odpowiada w układzie współrzędnych punkt
. Początek toru postanowiono zlokalizować na brzegu jeziora w miejscu, któremu odpowiada w układzie współrzędnych punkt 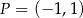 .
.
Niech 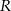 będzie punktem leżącym na wykresie funkcji
będzie punktem leżącym na wykresie funkcji 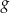 . Wykaż, że odległość punktu
. Wykaż, że odległość punktu 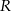 od punktu
od punktu 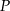 wyraża się wzorem
wyraża się wzorem
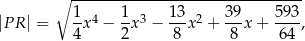
gdzie  jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 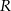 .
.
Koniec toru regatowego należy umieścić na linii brzegowej. Oblicz współrzędne punktu 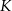 , w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca
, w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca 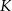 toru od początku
toru od początku 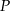 ) była możliwie największa. Oblicz długość najdłuższego toru.
) była możliwie największa. Oblicz długość najdłuższego toru.
Przy rozwiązywaniu zadania możesz skorzystać z tego, że odległość dowolnego punktu 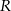 leżącego na wykresie funkcji
leżącego na wykresie funkcji 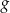 od punktu
od punktu 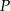 wyraża się wzorem
wyraża się wzorem
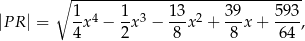
gdzie  jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 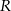 .
.
Rozwiąż równanie
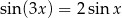
w zbiorze ![[0,π ]](https://img.zadania.info/zes/0083221/HzesT48x.gif) .
.
Dany jest trapez równoramienny 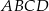 o obwodzie
o obwodzie 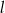 i podstawach
i podstawach 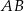 oraz
oraz 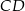 takich, że
takich, że 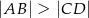 . Trapez jest opisany na okręgu i wpisany w okrąg, a przekątna
. Trapez jest opisany na okręgu i wpisany w okrąg, a przekątna 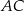 trapezu ma długość
trapezu ma długość 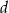 (zobacz rysunek).
(zobacz rysunek).
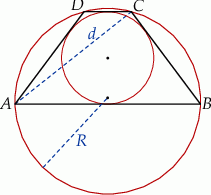
Wykaż, że promień 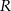 okręgu opisanego na trapezie
okręgu opisanego na trapezie 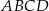 jest równy
jest równy 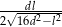 .
.
W kartezjańskim układzie współrzędnych 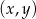 punkt
punkt 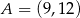 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 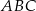 . Prosta
. Prosta 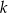 o równaniu
o równaniu 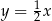 zawiera dwusieczną kąta
zawiera dwusieczną kąta 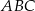 tego trójkąta. Okrąg
tego trójkąta. Okrąg 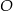 o równaniu
o równaniu 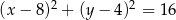 jest wpisany w ten trójkąt. Oblicz współrzędne punktu styczności prostej przechodzącej przez wierzchołki
jest wpisany w ten trójkąt. Oblicz współrzędne punktu styczności prostej przechodzącej przez wierzchołki 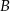 i
i 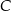 tego trójkąta z okręgiem
tego trójkąta z okręgiem 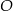 .
.
Dany jest ostrosłup prawidłowy czworokątny 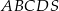 o podstawie
o podstawie 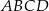 i polu powierzchni bocznej równym
i polu powierzchni bocznej równym 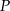 . Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka
. Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka 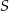 ma miarę
ma miarę 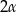 . Objętość tego ostrosłupa jest równa
. Objętość tego ostrosłupa jest równa 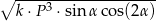 , gdzie
, gdzie 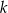 jest stałym współczynnikiem liczbowym. Oblicz współczynnik
jest stałym współczynnikiem liczbowym. Oblicz współczynnik 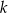 .
.
Egzamin składa się z 15 zadań zamkniętych. Do każdego zadania podano cztery odpowiedzi, z których tylko jedna okazuje się poprawna. Zdający zalicza egzamin, jeśli udzieli poprawnych odpowiedzi w co najmniej 11 zadaniach. Pewien student przystąpił nieprzygotowany do egzaminu i w każdym zadaniu wybierał losowo odpowiedź. Przyjmij, że w każdym zadaniu wybór każdej z odpowiedzi przez studenta jest równo prawdopodobny. Oblicz prawdopodobieństwo zdarzenia, że ten student zaliczył egzamin.

