/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 9 marca 2019 Czas pracy: 180 minut
Zadania zamknięte
Niech 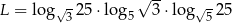 . Wtedy
. Wtedy
A) 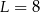 B)
B) 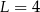 C)
C) 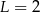 D)
D) 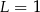
Liczba 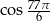 jest równa
jest równa
A) 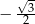 B)
B) 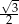 C)
C) 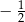 D)
D) 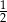
Odległość pomiędzy prostymi równoległymi 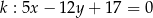 i
i 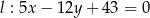 jest równa
jest równa
A) 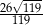 B)
B) 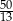 C) 1 D) 2
C) 1 D) 2
Granica 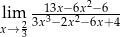 jest równa
jest równa
A) 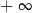 B) 0 C)
B) 0 C) 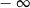 D)
D) 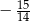
Funkcja 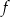 jest określona wzorem
jest określona wzorem 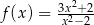 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 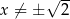 . Wówczas pochodna tej funkcji dla argumentu
. Wówczas pochodna tej funkcji dla argumentu 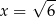 jest równa
jest równa
A) 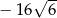 B)
B) 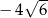 C)
C) 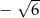 D)
D) 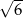
Zadania otwarte
Wyznacz wszystkie wartości parametru 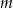 , dla których zbiór rozwiązań nierówności
, dla których zbiór rozwiązań nierówności
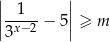
jest przedziałem postaci 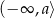 .
.
Liczby 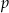 i
i 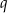 są pierwiastkami równania
są pierwiastkami równania 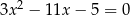 . Wykaż, że pierwiastkami równania
. Wykaż, że pierwiastkami równania 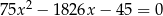 są liczby
są liczby 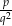 i
i 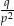 .
.
Ciąg 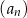 jest ciągiem arytmetycznym o różnicy 2 i czwartym wyrazie równym
jest ciągiem arytmetycznym o różnicy 2 i czwartym wyrazie równym 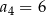 . Ciąg
. Ciąg 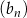 dla dowolnego
dla dowolnego 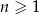 spełnia warunek
spełnia warunek 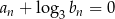 . Oblicz granicę
. Oblicz granicę
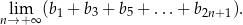
Na przedłużeniu przeciwprostokątnej 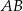 trójkąta prostokątnego
trójkąta prostokątnego 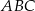 wybrano punkt
wybrano punkt 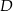 tak, że
tak, że 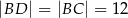 . Oblicz długość odcinka
. Oblicz długość odcinka 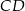 jeżeli
jeżeli 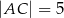 .
.
Wyznacz wzór funkcji kwadratowej 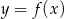 wiedząc, że jest on styczny do prostej
wiedząc, że jest on styczny do prostej 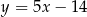 w punkcie
w punkcie 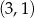 oraz przechodzi przez punkt
oraz przechodzi przez punkt 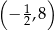 .
.
Spośród liczb naturalnych ośmiocyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby o sumie cyfr równej 4, jeżeli wiadomo, że żadna cyfra wylosowanej liczby nie jest równa 2, 3, 6 ani 8.
Udowodnij, że dla każdej liczby całkowitej 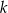 i dla każdej liczby całkowitej
i dla każdej liczby całkowitej 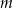 liczba
liczba 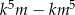 jest podzielna przez 10.
jest podzielna przez 10.
Rozwiąż równanie 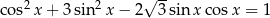 w przedziale
w przedziale 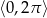 .
.
Podstawą ostrosłupa 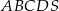 jest prostokąt
jest prostokąt 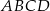 , w którym
, w którym 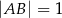 ,
, 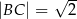 . Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
. Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
Trapez równoramienny 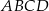 o podstawach
o podstawach 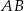 i
i 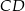 jest opisany na okręgu o równaniu
jest opisany na okręgu o równaniu 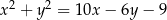 . Okrąg ten przecina boki
. Okrąg ten przecina boki 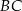 i
i 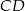 tego trapezu odpowiednio w punktach
tego trapezu odpowiednio w punktach 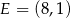 i
i 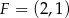 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 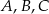 i
i 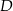 tego trapezu.
tego trapezu.
Okno na poddaszu ma mieć kształt trapezu równoramiennego, którego przekątna ma długość 6 dm. Oblicz, jakie jest największe możliwe pole powierzchni tego okna.

