/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 17 marca 2012 Czas pracy: 180 minut
Która z liczb jest większa 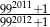 , czy
, czy 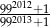 ?
?
Punkt 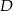 leży na boku
leży na boku 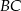 trójkąta równoramiennego, w którym
trójkąta równoramiennego, w którym 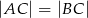 . Odcinek
. Odcinek 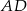 dzieli trójkąt
dzieli trójkąt 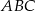 na dwa trójkąty równoramienne takie, że
na dwa trójkąty równoramienne takie, że 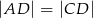 i
i  . Wykaż, że
. Wykaż, że 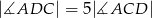 .
.
Ciąg 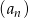 dla
dla 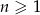 jest ciągiem arytmetycznym oraz
jest ciągiem arytmetycznym oraz 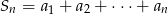 dla
dla 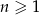 . Wykaż, że jeżeli spełniony jest warunek
. Wykaż, że jeżeli spełniony jest warunek 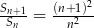 dla
dla 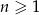 , to spełniony jest również warunek
, to spełniony jest również warunek 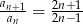 .
.
Rozwiąż równanie 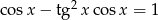 w przedziale
w przedziale 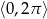 .
.
Wykaż, że równanie 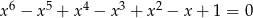 nie ma rozwiązań rzeczywistych.
nie ma rozwiązań rzeczywistych.
Dla jakich wartości 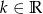 równanie
równanie 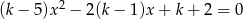 ma dwa różne pierwiastki dodatnie?
ma dwa różne pierwiastki dodatnie?
Środkowa 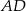 trójkąta równoramiennego
trójkąta równoramiennego 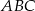 ma długość
ma długość 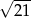 , a jego podstawa
, a jego podstawa 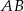 tworzy z ramieniem kąt o mierze
tworzy z ramieniem kąt o mierze 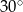 . Oblicz pole trójkąta
. Oblicz pole trójkąta 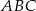 .
.
W pewnym budynku biurowym przydzielono pracownikom pięciocyfrowe kody bezpieczeństwa, przy czym każdy kod musiał spełniać następujące dwa warunki:
(1) kod musi zawierać co najmniej 3 różne cyfry
(2) kod musi zawierać co najmniej jedną cyfrę parzystą i co najmniej jedną cyfrę nieparzystą.
Ile jest kodów spełniających powyższe warunki?
Napisz równanie okręgu, który jest styczny do prostej 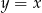 w punkcie
w punkcie 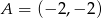 , oraz który odcina z prostej
, oraz który odcina z prostej 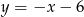 cięciwę o długości 8.
cięciwę o długości 8.
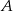 i
i 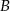 są takim zdarzeniami losowymi zawartymi w
są takim zdarzeniami losowymi zawartymi w 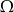 , że
, że 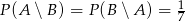 i
i 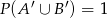 . Oblicz
. Oblicz 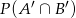 .
.
Dany jest ostrosłup prawidłowy czworokątny 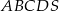 o podstawie
o podstawie 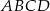 . Pole trójkąta
. Pole trójkąta 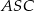 jest równe 120, a cosinus kąta
jest równe 120, a cosinus kąta 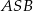 jest równy
jest równy 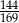 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.

