/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 19 marca 2011 Czas pracy: 170 minut
Zadania zamknięte
Na koncert sprzedano 680 biletów, w tym 306 na miejsca siedzące. Jaki procent sprzedanych biletów stanowiły bilety na miejsca siedzące?
A) 63% B) 45% C) 33% D) 22%
Wynikiem działania 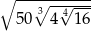 jest
jest
A) 100 B) 20 C) 10 D) 15
Przedział 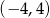 jest zbiorem liczb spełniających nierówność
jest zbiorem liczb spełniających nierówność
A) 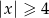 B)
B) 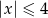 C)
C) 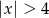 D)
D) 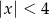
Liczba 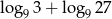 jest równa
jest równa
A) 2 B) 1 C) 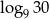 D)
D) 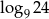
Kąt  jest ostry i
jest ostry i 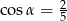 . Wtedy
. Wtedy 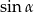 jest równy
jest równy
A) 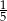 B)
B) 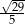 C)
C)  D)
D) 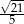
Kwadrat liczby 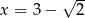 jest równy
jest równy
A) 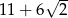 B)
B) 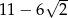 C) 7 D) 11
C) 7 D) 11
Wykres funkcji 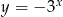 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) I i II B) II i III C) III i IV D) IV i I
Korzystając z danego wykresu funkcji 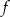 , wskaż nierówność prawdziwą
, wskaż nierówność prawdziwą
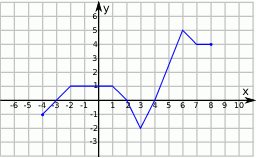
A) 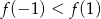 B)
B) 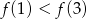 C)
C) 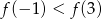 D)
D) 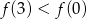
Zbiorem wartości funkcji 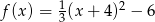 jest
jest
A) 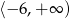 B)
B) 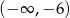 C)
C) 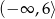 D)
D) 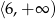
Rozwiązaniem równania 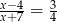 jest liczba
jest liczba
A)  B) 5 C) 37 D)
B) 5 C) 37 D) 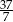
Zbiór rozwiązań nierówności 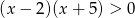 przedstawiony jest na rysunku
przedstawiony jest na rysunku
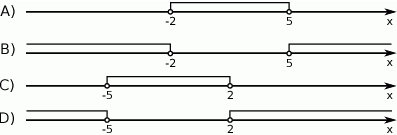
Suma dwudziestu początkowych wyrazów ciągu arytmetycznego 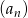 danego wzorem
danego wzorem 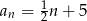 jest równa
jest równa
A) 205 B) 410 C) 200 D) 210
Liczba przekątnych sześciokąta foremnego jest równa
A) 9 B) 14 C) 18 D) 6
Prosta o równaniu 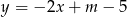 przechodzi przez punkt
przechodzi przez punkt 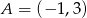 . Wtedy
. Wtedy
A) 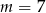 B)
B) 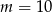 C)
C) 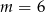 D)
D) 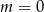
Proste o równaniach 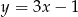 oraz
oraz 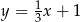
A) pokrywają się
B) przecinają się pod kątem innym niż prosty
C) są prostopadłe
D) są równoległe i różne
Wybieramy jedną liczbę ze zbioru 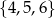 i jedną liczbę ze zbioru
i jedną liczbę ze zbioru 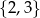 . Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
. Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
A) 6 B) 5 C) 4 D) 3
Punkty 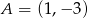 i
i 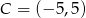 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 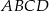 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 10 B) 25 C) 50 D) 100
Dane są punkty 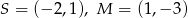 . Równanie okręgu o środku
. Równanie okręgu o środku 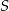 i przechodzącego przez punkt
i przechodzącego przez punkt 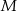 ma postać
ma postać
A) 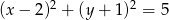
B) 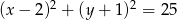
C) 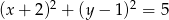
D) 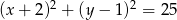
Pole powierzchni całkowitej prostopadłościanu o wymiarach 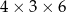 jest równe
jest równe
A) 94 B) 54 C) 108 D) 72
Na loterii jest 20 losów, z których 8 jest wygrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A)  B)
B)  C)
C) 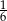 D)
D) 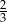
Zadania otwarte
Rozwiąż nierówność 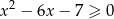 .
.
Rozwiąż równanie 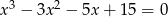 .
.
Wykaż, że dla każdego 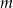 ciąg
ciąg 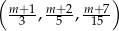 jest arytmetyczny.
jest arytmetyczny.
Wykaż, że dla dowolnych liczb dodatnich  i
i 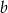 spełniona jest równość
spełniona jest równość
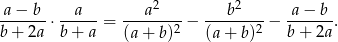
Dany jest równoległobok 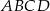 . Okręgi o średnicach
. Okręgi o średnicach 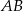 i
i 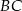 przecinają się w punktach
przecinają się w punktach 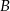 i
i 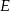 .
.
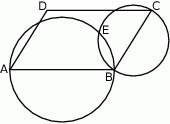
Wykaż, że punkty 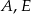 i
i 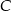 leżą na jednej prostej.
leżą na jednej prostej.
Oblicz, ile jest liczb naturalnych czterocyfrowych, w których zapisie pierwsza cyfra jest liczbą podzielną przez 3, a pozostałe są parzyste.
Punkty 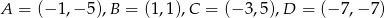 są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
Wyznacz wzór funkcji 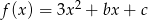 w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania
w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania 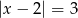 .
.
Samochód przejechał trasę długości 84 km. Gdyby jechał ze średnią prędkością większą o 12 km/h, to przejechałby tę trasę w czasie o 21 minut krótszym. Oblicz, z jaką średnią prędkością jechał ten samochód.
W trapezie równoramiennym 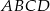 ramię ma długość 13. Obwód tego trapezu jest równy 52. Wiedząc, że tangens kąta ostrego w trapezie
ramię ma długość 13. Obwód tego trapezu jest równy 52. Wiedząc, że tangens kąta ostrego w trapezie 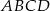 jest równy
jest równy 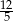 , oblicz długości jego podstaw.
, oblicz długości jego podstaw.

