/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki poziom podstawowy
(technikum) grupa I 25 lutego 2015 Czas pracy: 170 minut
Zadania zamknięte
Zbiorem rozwiązań nierówności 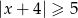 jest:
jest:
A) 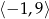 B)
B) 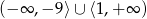 C)
C) 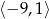 D)
D) 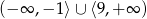
Liczba 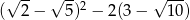 jest równa
jest równa
A) 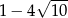 B) 13 C)
B) 13 C) 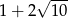 D) 1
D) 1
Liczba 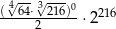 jest równa
jest równa
A) 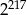 B)
B) 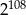 C)
C) 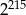 D) 1
D) 1
Liczba odwrotna do liczby 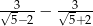 jest liczba
jest liczba
A) 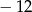 B)
B) 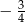 C)
C) 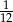 D)
D) 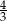
Suma 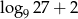 jest równa
jest równa
A) 5 B) 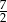 C)
C) 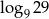 D)
D) 
Magda wydała na książkę połowę kwoty otrzymanej od mamy, a za 40% tego, co jej zostało kupiła bilet do kina. Ile procent kwoty otrzymanej od mamy pozostało Magdzie?
A) 30% B) 60% C) 10% D) 20%
Wspólnym pierwiastkiem równań 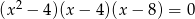 oraz
oraz 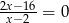 jest liczba
jest liczba
A) 2 B) 4 C) 8 D) 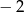
Funkcja liniowa 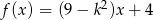 jest rosnąca wtedy, gdy
jest rosnąca wtedy, gdy
A) 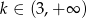 B)
B) 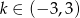 C)
C) 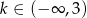 D)
D) 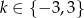
Zbiorem wartości funkcji kwadratowej 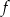 jest przedział
jest przedział 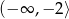 . Funkcja
. Funkcja 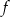 może być określona wzorem
może być określona wzorem
A) 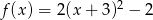
B) 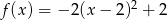
C) 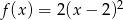
D) 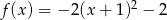
Oś symetrii paraboli, która jest wykresem funkcji 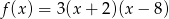 ma równanie
ma równanie
A) 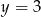 B)
B) 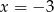 C)
C) 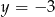 D)
D) 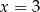
Przekątne rombu 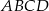 przecinają się w punkcie
przecinają się w punkcie 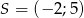 . Przekątna
. Przekątna 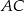 zawarta jest w prostej o równaniu
zawarta jest w prostej o równaniu 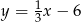 . Wskaż równanie prostej zawierającej przekątną
. Wskaż równanie prostej zawierającej przekątną 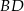 tego rombu.
tego rombu.
A) 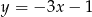 B)
B) 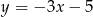 C)
C) 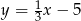 D)
D) 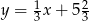
Liczby 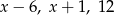 są trzema kolejnymi wyrazami ciągu arytmetycznego. Liczba
są trzema kolejnymi wyrazami ciągu arytmetycznego. Liczba  jest równa
jest równa
A) 4 B) 8,5 C) 1 D) 5
Ciąg geometryczny 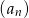 określony jest wzorem
określony jest wzorem 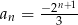 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 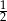 B)
B) 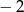 C)
C) 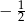 D) 2
D) 2
Pole trójkąta 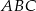 jest równe
jest równe 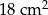 . Trójkąt
. Trójkąt 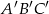 jest podobny do trójkąta
jest podobny do trójkąta 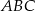 w skali
w skali 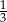 . Pole trójkąta
. Pole trójkąta 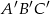 jest równe
jest równe
A) 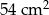 B)
B) 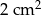 C)
C) 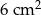 D)
D) 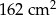
Kąt  jest ostry i
jest ostry i 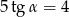 . Wartość wyrażenia
. Wartość wyrażenia 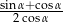 jest równa
jest równa
A)  B)
B)  C)
C) 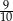 D)
D) 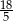
Punkt 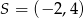 jest środkiem okręgu. Na okręgu leży punkt
jest środkiem okręgu. Na okręgu leży punkt 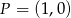 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 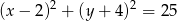
B) 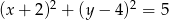
C) 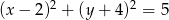
D) 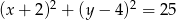
Punkt 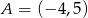 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 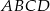 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie 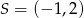 . Wierzchołek
. Wierzchołek 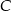 ma współrzędne
ma współrzędne
A) 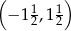 B)
B) 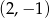 C)
C) 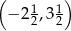 D)
D) 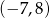
Kąt wpisany oparty jest na łuku, którego długość jest równa 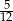 długości okręgu. Miara tego kąta wynosi
długości okręgu. Miara tego kąta wynosi
A) 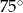 B)
B) 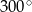 C)
C) 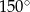 D)
D) 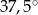
Jeżeli prawdopodobieństwo zdarzenia losowego 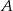 jest 5 razy większe od prawdopodobieństwa zdarzenia przeciwnego do zdarzenia
jest 5 razy większe od prawdopodobieństwa zdarzenia przeciwnego do zdarzenia 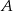 , to prawdopodobieństwo zdarzenia
, to prawdopodobieństwo zdarzenia 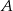 jest równe
jest równe
A)  B)
B) 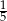 C)
C)  D)
D) 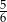
Ostrosłup ma 15 wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa
A) 15 B) 14 C) 28 D) 30
Średnia arytmetyczna liczb: 3, 1, 6, 5, 2, 4,  , 2, 3, 8 wynosi 4. Medianą tego zbioru liczb jest
, 2, 3, 8 wynosi 4. Medianą tego zbioru liczb jest
A) 3,5 B) 3 C) 4,5 D) 4
Powierzchnia boczna walca po rozwinięciu jest kwadratem o polu 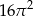 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 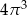 B)
B) 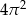 C)
C) 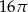 D)
D) 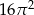
Dłuższy bok prostokąta ma długość 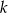 . Przekątna prostokąta tworzy z krótszym bokiem kąt
. Przekątna prostokąta tworzy z krótszym bokiem kąt  . Długość przekątnej prostokąta wynosi
. Długość przekątnej prostokąta wynosi
A) 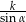 B)
B) 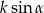 C)
C) 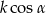 D)
D) 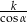
Do wykresu funkcji liniowej 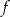 należy punkt
należy punkt 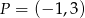 , a jej miejscem zerowym jest
, a jej miejscem zerowym jest 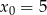 . Wzór funkcji
. Wzór funkcji 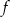 ma postać
ma postać
A) 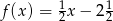 B)
B) 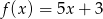 C)
C) 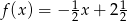 D)
D) 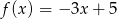
Liczb dwucyfrowych większych od 50 o nieparzystych cyfrach jest
A) 12 B) 25 C) 49 D) 15
Zadania otwarte
Wyznacz zbiór argumentów, dla których funkcja 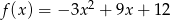 przyjmuje wartości nieujemne.
przyjmuje wartości nieujemne.
Rozwiąż równanie 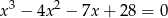 .
.
Wykaż, że jeśli 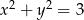 i
i 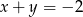 , to
, to 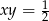 .
.
W ciągu arytmetycznym 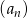 pierwszy wyraz
pierwszy wyraz 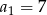 , a czwarty wyraz
, a czwarty wyraz 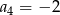 . Oblicz sumę osiemnastu początkowych wyrazów tego ciągu.
. Oblicz sumę osiemnastu początkowych wyrazów tego ciągu.
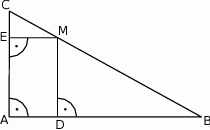
W trójkącie prostokątnym 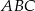 punkt
punkt 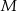 leży na przeciwprostokątnej
leży na przeciwprostokątnej 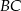 . Z punktu
. Z punktu 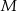 poprowadzono odcinki
poprowadzono odcinki 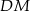 i
i 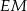 prostopadłe odpowiednio do przyprostokątnych
prostopadłe odpowiednio do przyprostokątnych 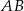 i
i 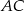 (rysunek). Udowodnij, że
(rysunek). Udowodnij, że 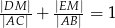 .
.
Ze zbioru liczb 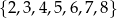 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 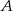 polegającego na wylosowaniu liczb, z których pierwsza jest o 2 mniejsza od drugiej.
polegającego na wylosowaniu liczb, z których pierwsza jest o 2 mniejsza od drugiej.
W trapezie równoramiennym 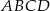 przekątna
przekątna 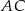 jest prostopadła do ramienia i tworzy z dłuższą podstawą
jest prostopadła do ramienia i tworzy z dłuższą podstawą 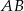 trapezu kąt o mierze
trapezu kąt o mierze 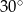 . Oblicz pole powierzchni tego trapezu wiedząc, że długość przekątnej
. Oblicz pole powierzchni tego trapezu wiedząc, że długość przekątnej 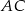 wynosi
wynosi 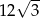 .
.
Długości trzech krawędzi wychodzących z jednego wierzchołka prostopadłościanu są kolejnymi liczbami parzystymi. Pole powierzchni całkowitej prostopadłościanu wynosi 208. Oblicz objętość tego prostopadłościanu.
Rowerzysta wybrał się na wycieczkę nad jezioro i z powrotem. W obie strony jechał dokładnie tą samą trasą i łącznie pokonał 60 km. Jadąc z domu nad jezioro poruszał się z prędkością o 2 km/h większą niż w drodze powrotnej i pokonał trasę w czasie o 10 minut krótszym niż trasę powrotną. Z jaką prędkością jechał rowerzysta w drodze powrotnej i ile czasu zajął mu powrót do domu znad jeziora?

