/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 2 kwietnia 2016 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 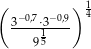 jest równa
jest równa
A) 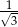 B)
B) 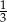 C) 3 D)
C) 3 D) 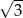
Każdą krawędź graniastosłupa prostego o podstawie będącej sześciokątem wydłużono dwukrotnie. W wyniku tej zmiany pole powierzchni graniastosłupa zwiększyło się o
A) 100% B) 300% C) 200% D) 400%
Kwotę 2000 zł ulokowano w banku na roczną lokatę oprocentowaną w wysokości 3% w stosunku rocznym. Po zakończeniu lokaty od naliczonych odsetek odprowadzany jest podatek w wysokości 19%. Maksymalna kwota, jaką po upływie roku będzie można wypłacić z banku, jest równa
A) 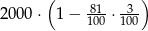
B) 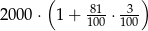
C) 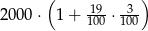
D) 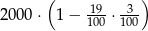
Wyrażenie 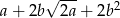 może być przekształcone do postaci
może być przekształcone do postaci
A) 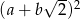 B)
B) 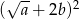 C)
C) 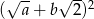 D)
D) 
Wartość wyrażenia 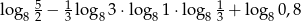 jest równa
jest równa
A) 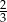 B) 0 C)
B) 0 C) 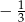 D)
D) 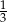
Wyrażenie 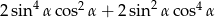 może być przekształcone do postaci
może być przekształcone do postaci
A) 2 B) 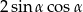 C)
C) 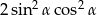 D)
D) 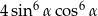
Równanie 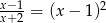
A) nie ma rozwiązań.
B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania.
D) ma dokładnie trzy rozwiązania.
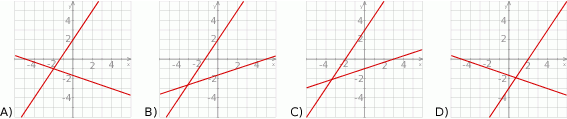
Na jednym z poniższych rysunków przedstawiono interpretację geometryczną układu równań 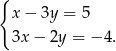 Wskaż ten rysunek:
Wskaż ten rysunek:
Liczby 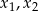 są rozwiązaniami równania
są rozwiązaniami równania 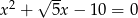 . Liczba
. Liczba 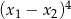 jest równa
jest równa
A) 45 B) 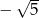 C) 2025 D) 10
C) 2025 D) 10
Funkcja liniowa 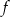 określona wzorem
określona wzorem 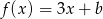 ma takie samo miejsce zerowe, jakie ma funkcja liniowa
ma takie samo miejsce zerowe, jakie ma funkcja liniowa 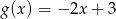 . Stąd wynika, że
. Stąd wynika, że
A) 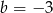 B)
B) 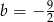 C)
C) 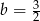 D)
D) 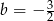
Jednym z miejsc zerowych funkcji kwadratowej 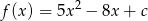 jest liczba
jest liczba  . Wówczas
. Wówczas  jest równe
jest równe
A) 1 B) 0 C) 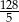 D)
D) 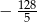
Gdy przesuniemy wykres funkcji 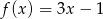 o 4 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
o 4 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
A) 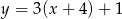 B)
B) 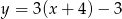 C)
C) 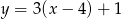 D)
D) 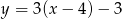
Ciąg geometryczny 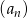 jest określony wzorem
jest określony wzorem 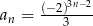 dla
dla 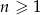 . Suma jedenastu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma jedenastu początkowych kolejnych wyrazów tego ciągu jest równa
A) 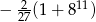 B)
B) 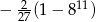 C)
C) 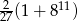 D)
D) 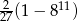
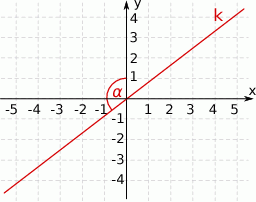
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy 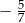 . Wskaż równanie prostej
. Wskaż równanie prostej 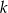 .
.
A) 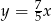 B)
B) 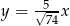 C)
C) 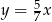 D)
D) 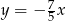
W ciągu arytmetycznym 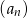 , określonym dla
, określonym dla 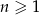 , dane są dwa wyrazy:
, dane są dwa wyrazy: 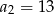 i
i 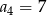 . Suma czterech początkowych wyrazów tego ciągu jest równa
. Suma czterech początkowych wyrazów tego ciągu jest równa
A) 92 B) 39 C) 46 D) 50
Liczby naturalne 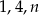 są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
A) 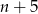 B)
B) 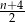 C) 4 D)
C) 4 D) 
Pole rombu o boku 6 i kącie rozwartym 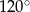 jest równe
jest równe
A) 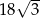 B) 18 C)
B) 18 C) 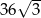 D) 36
D) 36
Punkty 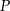 i
i 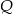 są środkami boków
są środkami boków 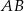 i
i 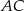 trójkąta
trójkąta 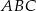 . Bok
. Bok 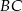 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu 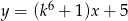 , a punkty
, a punkty 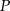 i
i 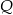 leżą na prostej
leżą na prostej 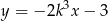 . Wynika stąd, że
. Wynika stąd, że
A) 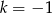 B)
B) 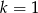 C)
C) 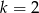 D)
D) 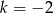
W trójkącie prostokątnym 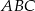 , w którym
, w którym 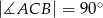 , na boku
, na boku 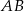 wybrano punkt
wybrano punkt 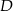 taki, że
taki, że 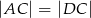 (zobacz rysunek).
(zobacz rysunek).
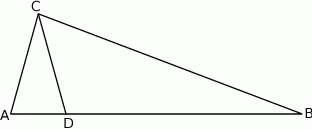
Wynika stąd, że różnica miar kątów 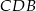 i
i 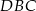 jest równa
jest równa
A) 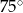 B)
B) 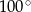 C)
C) 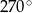 D)
D) 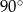
Punkty 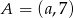 i
i 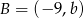 są końcami średnicy okręgu o środku
są końcami średnicy okręgu o środku 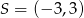 . Wtedy
. Wtedy
A) 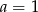 B)
B) 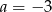 C)
C) 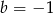 D)
D) 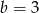
W ostrosłupie prawidłowym czworokątnym, w którym wszystkie krawędzie mają tę samą długość, kąt między wysokością ostrosłupa, a jego krawędzią boczną ma miarę
A) 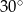 B)
B) 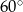 C)
C) 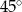 D)
D) 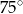
Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości 4. Objętość tego stożka jest równa
A) 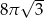 B)
B) 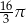 C)
C) 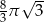 D)
D) 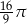
Średnia arytmetyczna zestawu danych: 1, 3, 6, 7,  jest równa
jest równa  , natomiast średnia arytmetyczna zestawu danych: 1, 3, 7, 7,
, natomiast średnia arytmetyczna zestawu danych: 1, 3, 7, 7,  ,
, 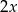 jest równa
jest równa 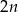 . Wynika stąd, że
. Wynika stąd, że
A) 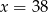 B)
B) 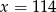 C)
C) 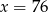 D)
D) 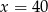
Wykresy funkcji 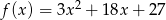 i
i 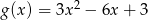 są symetryczne względem prostej
są symetryczne względem prostej
A) 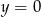 B)
B) 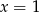 C)
C) 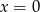 D)
D) 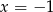
W pewnej loterii fantowej przygotowano dwie urny z losami, przy czym w drugiej urnie było trzy razy więcej losów niż w pierwszej urnie. Prawdopodobieństwo wybrania losu wygrywającego z pierwszej urny jest równe 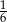 , a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe
, a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe 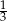 . Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
. Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
A)  B)
B) 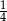 C)
C) 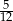 D)
D) 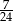
Zadania otwarte
Rozwiąż równanie 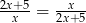 , gdzie
, gdzie 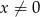 i
i 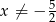 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 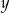 prawdziwa jest nierówność
prawdziwa jest nierówność 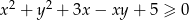 .
.
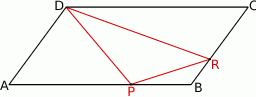
W równoległoboku 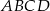 punkt
punkt 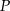 jest takim punktem boku
jest takim punktem boku 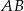 , że
, że 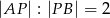 . Punkt
. Punkt 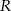 jest takim punktem boku
jest takim punktem boku 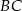 , że
, że 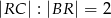 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 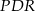 jest 5 razy większe od pola trójkąta
jest 5 razy większe od pola trójkąta 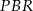 .
.
Uczeń otrzymał pięć ocen: 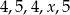 . Średnia arytmetyczna tych ocen jest równa 4,4. Oblicz
. Średnia arytmetyczna tych ocen jest równa 4,4. Oblicz  i medianę tych pięciu ocen.
i medianę tych pięciu ocen.
Ze zbioru liczb naturalnych dwucyfrowych losowo wybieramy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 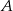 polegającego na tym, że otrzymamy liczbę podzielną przez 6 lub liczbę podzielną przez 9.
polegającego na tym, że otrzymamy liczbę podzielną przez 6 lub liczbę podzielną przez 9.
Funkcja kwadratowa 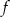 dla
dla 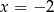 przyjmuje wartość największą równą 1. Do wykresu funkcji
przyjmuje wartość największą równą 1. Do wykresu funkcji 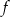 należy punkt
należy punkt 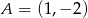 . Zapisz wzór funkcji kwadratowej
. Zapisz wzór funkcji kwadratowej 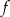 .
.
Pole podstawy graniastosłupa prawidłowego czworokątnego jest równe 16. Przekątna graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem, którego sinus jest równy 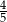 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
Boki 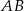 i
i 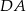 równoległoboku
równoległoboku 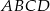 są zawarte odpowiednio w prostych o równaniach
są zawarte odpowiednio w prostych o równaniach 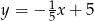 i
i 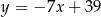 . Napisz równanie prostej zawierającej przekątną
. Napisz równanie prostej zawierającej przekątną 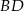 tego równoległoboku, jeżeli jego środek ma współrzędne
tego równoległoboku, jeżeli jego środek ma współrzędne 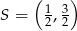 .
.
Niech 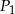 będzie prostokątem o polu
będzie prostokątem o polu 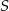 i stosunku długości boków równym 3:2. Konstruujemy kolejno prostokąty
i stosunku długości boków równym 3:2. Konstruujemy kolejno prostokąty 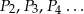 podobne do prostokąta
podobne do prostokąta 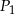 takie, że dłuższy bok kolejnego prostokąta jest równy krótszemu bokowi poprzedniego prostokąta. Oblicz sumę pól prostokątów
takie, że dłuższy bok kolejnego prostokąta jest równy krótszemu bokowi poprzedniego prostokąta. Oblicz sumę pól prostokątów 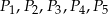 .
.

