/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki (stara formuła)
poziom rozszerzony 9 maja 2018 Czas pracy: 180 minut
Rozwiąż równanie 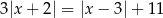 .
.
Liczby 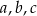 , spełniające warunek
, spełniające warunek 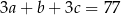 , są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Ciąg
, są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Ciąg 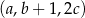 jest geometryczny. Wyznacz liczby
jest geometryczny. Wyznacz liczby 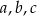 oraz podaj wyrazy ciągu geometrycznego.
oraz podaj wyrazy ciągu geometrycznego.
Dany jest czworokąt wypukły 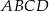 , w którym
, w którym 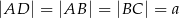 ,
, 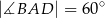 i
i 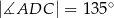 . Oblicz pole czworokąta
. Oblicz pole czworokąta 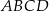 .
.
Z liczb ośmioelementowego zbioru 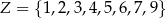 tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
Trójkąt 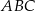 jest ostrokątny oraz
jest ostrokątny oraz 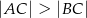 . Dwusieczna
. Dwusieczna 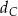 kąta
kąta 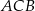 przecina bok
przecina bok 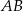 w punkcie
w punkcie 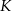 . Punkt
. Punkt 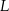 jest obrazem punktu
jest obrazem punktu 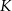 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 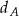 kąta
kąta 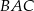 , punkt
, punkt 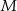 jest obrazem punktu
jest obrazem punktu 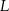 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 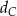 kąta
kąta 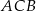 , a punkt
, a punkt 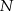 jest obrazem punktu
jest obrazem punktu 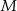 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 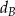 kąta
kąta 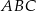 (zobacz rysunek).
(zobacz rysunek).
Udowodnij, że na czworokącie 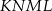 można opisać okrąg.
można opisać okrąg.
Udowodnij, że dla każdej liczby całkowitej 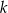 i dla każdej liczby całkowitej
i dla każdej liczby całkowitej 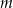 liczba
liczba 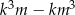 jest podzielna przez 6.
jest podzielna przez 6.
Rozwiąż równanie 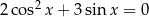 w przedziale
w przedziale 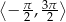 .
.
Liczba  jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 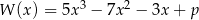 . Wyznacz pozostałe pierwiastki tego wielomianu i rozwiąż nierówność
. Wyznacz pozostałe pierwiastki tego wielomianu i rozwiąż nierówność 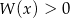 .
.
Wyznacz wszystkie wartości parametru 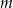 , dla których równanie
, dla których równanie 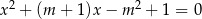 ma dwa rozwiązania rzeczywiste
ma dwa rozwiązania rzeczywiste 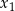 i
i 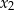
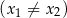 , spełniające warunek
, spełniające warunek 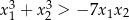 .
.
Punkt 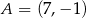 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 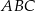 , w którym
, w którym 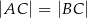 . Obie współrzędne wierzchołka
. Obie współrzędne wierzchołka  są liczbami ujemnymi. Okrąg wpisany w trójkąt
są liczbami ujemnymi. Okrąg wpisany w trójkąt 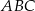 ma równanie
ma równanie 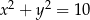 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 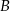 i
i 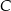 tego trójkąta.
tego trójkąta.
Przekrój ostrosłupa prawidłowego trójkątnego 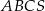 płaszczyzną przechodzącą przez wierzchołek
płaszczyzną przechodzącą przez wierzchołek 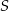 i wysokości dwóch ścian bocznych jest trójkątem równobocznym. Krawędź boczna tego ostrosłupa ma długość
i wysokości dwóch ścian bocznych jest trójkątem równobocznym. Krawędź boczna tego ostrosłupa ma długość 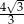 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.

