/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 27 kwietnia 2013 Czas pracy: 180 minut
Dla jakich wartości parametru 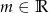 wierzchołek paraboli
wierzchołek paraboli 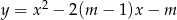 leży najbliżej osi
leży najbliżej osi 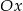 .
.
Rozwiąż równanie 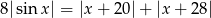 .
.
Wykaż, że jeżeli kąty 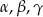 trójkąta
trójkąta 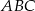 spełniają warunek
spełniają warunek 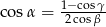 to trójkąt jest równoramienny.
to trójkąt jest równoramienny.
Wykaż, że jeżeli liczby dodatnie  i
i 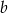 spełniają warunek
spełniają warunek
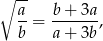
to 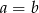 .
.
Wyznacz trzywyrazowy ciąg geometryczny, w którym suma trzech kolejnych wyrazów jest równa 84, a ich iloczyn jest równy 13824.
Wykaż, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność:
prawdziwa jest nierówność:
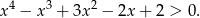
Wyznacz równanie okręgu o promieniu 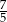 , który przechodzi przez punkty wspólne okręgów o równaniach
, który przechodzi przez punkty wspólne okręgów o równaniach 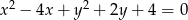 i
i 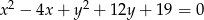 .
.
Dany jest trójkąt równoramienny 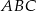 , w którym
, w którym 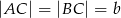 i
i 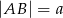 . Punkty
. Punkty 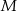 i
i 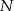 są rzutami prostopadłymi środka podstawy
są rzutami prostopadłymi środka podstawy 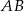 trójkąta na ramiona
trójkąta na ramiona 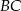 i
i 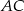 . Wyraź pole czworokąta
. Wyraź pole czworokąta 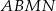 za pomocą
za pomocą  i
i 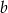 .
.
Z pudełka, w którym jest 15 kul ponumerowanych kolejnymi liczbami od 1 do 15, losujemy bez zwracania 5 kul. Oblicz, jakie jest prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna para kul z sumą numerów równą 16.
Suma długości krawędzi graniastosłupa prawidłowego czworokątnego jest równa 16. Dla jakiej długości krawędzi podstawy pole powierzchni całkowitej tego graniastosłupa będzie największe?

