/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom podstawowy grupa II 2 czerwca 2015 Czas pracy: 170 minut
Zadania zamknięte
Liczba 0,7 jest przybliżeniem liczby  . Błąd względny tego przybliżenia jest równy:
. Błąd względny tego przybliżenia jest równy:
A) 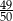 B)
B) 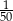 C)
C) 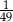 D)
D) 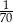
Liczba 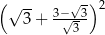 jest równa
jest równa
A) 11 B) 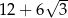 C)
C) 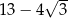 D) 3
D) 3
Liczba 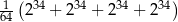 jest równa
jest równa
A) 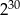 B)
B) 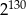 C)
C) 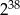 D)
D) 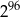
Liczba 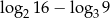 jest równa
jest równa
A) 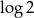 B)
B) 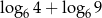 C)
C) 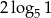 D)
D) 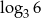
Układ równań 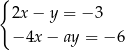 opisuje w układzie współrzędnych zbiór pusty dla
opisuje w układzie współrzędnych zbiór pusty dla
A) 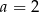 B)
B) 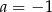 C)
C) 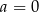 D)
D) 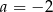
Suma wszystkich rozwiązań równania 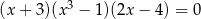 jest równa
jest równa
A) 2 B) 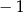 C)
C) 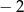 D) 0
D) 0
Wyrażenie 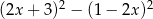 jest równe
jest równe
A) 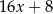 B)
B) 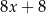 C)
C) 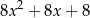 D)
D) 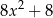
Liczba 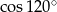 jest równa liczbie
jest równa liczbie
A) 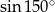 B)
B) 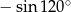 C)
C) 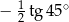 D)
D) 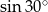
Zbiorem wartości funkcji kwadratowej 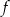 jest przedział
jest przedział 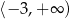 . Funkcja
. Funkcja 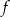 może być określona wzorem
może być określona wzorem
A) 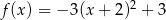
B) 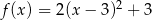
C) 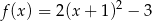
D) 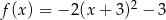
w trójkącie równoramiennym ramię ma długość 16 i tworzy z podstawą trójkąta kąt o mierze 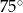 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 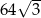 B)
B) 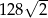 C) 128 D) 64
C) 128 D) 64
Punkt 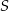 jest środkiem okręgu.
jest środkiem okręgu.
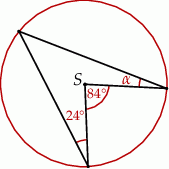
Miara kąta  wynosi
wynosi
A) 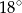 B)
B) 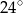 C)
C) 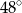 D)
D) 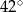
Jeżeli kąt  jest ostry i
jest ostry i 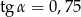 , to wartość wyrażenia
, to wartość wyrażenia 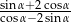 jest równa
jest równa
A) 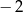 B)
B) 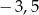 C) 11 D)
C) 11 D) 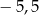
Ciąg 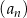 określony jest wzorem
określony jest wzorem 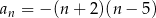 dla
dla 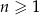 . Zatem
. Zatem
A) 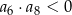 B)
B) 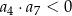 C)
C) 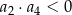 D)
D) 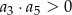
Pole trójkąta 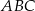 jest równe
jest równe 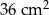 . Trójkąt
. Trójkąt 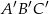 jest podobny do trójkąta
jest podobny do trójkąta 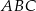 w skali
w skali 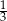 . Pole trójkąta
. Pole trójkąta 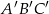 jest równe
jest równe
A) 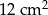 B)
B) 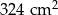 C)
C) 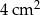 D)
D) 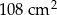
Pole koła opisanego na trójkącie równobocznym jest równe 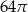 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość
A) 12 B) 24 C) 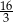 D) 16
D) 16
Punkt 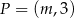 należy do wykresu funkcji liniowej
należy do wykresu funkcji liniowej 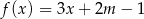 . Liczba
. Liczba 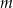 jest równa
jest równa
A) 1,25 B) 0,8 C) 8 D) 0,4
Jeden z kątów trójkąta jest trzy razy większy od drugiego. Miara trzeciego kąta jest o 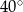 większa od miary najmniejszego kąta w tym trójkącie. Miary kątów tego trójkąta są równe
większa od miary najmniejszego kąta w tym trójkącie. Miary kątów tego trójkąta są równe
A) 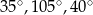 B)
B) 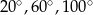 C)
C) 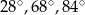 D)
D) 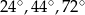
Zbiorem rozwiązań nierówności 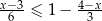 jest przedział
jest przedział
A) 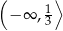 B)
B) 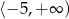 C)
C) 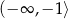 D)
D) 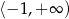
W klasie jest o 25% więcej chłopców niż dziewcząt. Jaką część wszystkich uczniów tej klasy stanowią chłopcy?
A) 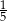 B)
B) 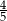 C)
C) 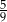 D)
D) 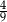
Funkcja kwadratowa określona jest wzorem 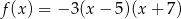 . Funkcja ta jest rosnąca w przedziale:
. Funkcja ta jest rosnąca w przedziale:
A) 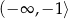 B)
B) 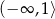 C)
C) 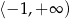 D)
D) 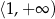
Różnica mniejszego i większego miejsca zerowego funkcji 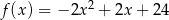 jest równa
jest równa
A) 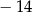 B)
B) 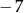 C) 14 D) 7
C) 14 D) 7
Dziedziną funkcji 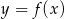 jest przedział
jest przedział 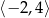 . Zatem dziedziną funkcji
. Zatem dziedziną funkcji 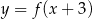 jest zbiór
jest zbiór
A) 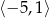 B)
B) 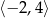 C)
C) 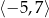 D)
D) 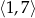
Drugi wyraz ciągu arytmetycznego jest równy 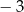 , a dziesiąty wyraz jest równy 21. Szósty wyraz tego ciągu ma wartość
, a dziesiąty wyraz jest równy 21. Szósty wyraz tego ciągu ma wartość
A) 6 B) 12 C) 8 D) 9
W rosnącym ciągu geometrycznym stosunek wyrazu czwartego do drugiego jest równy 8. Iloraz tego ciągu jest równy
A) 4 B) 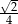 C)
C) 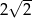 D)
D) 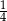
Zadania otwarte
Rozwiąż nierówność: 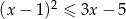 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 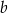 prawdziwa jest nierówność
prawdziwa jest nierówność 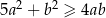 .
.
Wyznacz wszystkie liczby całkowite, które są rozwiązaniami równania: 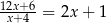 .
.
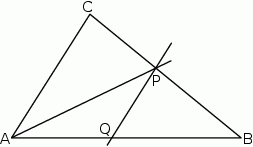
W trójkącie 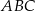 dwusieczna kąta
dwusieczna kąta 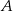 przecina bok
przecina bok 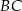 w punkcie
w punkcie 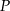 . Przez punkt
. Przez punkt 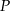 prowadzimy prostą równoległą do
prowadzimy prostą równoległą do 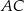 , przecinającą bok
, przecinającą bok 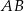 w punkcie
w punkcie 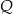 (rys.). Udowodnij, że
(rys.). Udowodnij, że 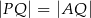 .
.
Oblicz najmniejszą i największą wartość funkcji 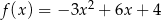 w przedziale
w przedziale 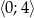 .
.
Przyprostokątna trójkąta prostokątnego ma długość 12. Miara kąta ostrego leżącego przy tej przyprostokątnej wynosi 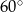 . Oblicz długość okręgu opisanego na tym trójkącie.
. Oblicz długość okręgu opisanego na tym trójkącie.
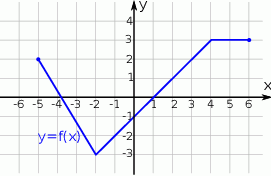
Na rysunku przedstawiony jest wykres funkcji 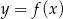 .
.
- Sporządź (na tym samym rysunku) wykres funkcji
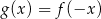 .
. - Podaj maksymalny przedział, w którym funkcja
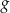 jest rosnąca.
jest rosnąca.
Dwa przeciwległe boki kwadratu wydłużono trzykrotnie, a każdy z dwóch pozostałych wydłużono o 2 cm. Pole otrzymanego prostokąta jest o 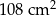 większe od pola kwadratu. Oblicz długości boków prostokąta.
większe od pola kwadratu. Oblicz długości boków prostokąta.
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 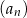 wyraża się wzorem
wyraża się wzorem 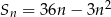 , gdzie
, gdzie 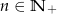 . Oblicz
. Oblicz  wiedząc, że liczby:
wiedząc, że liczby: 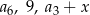 w podanej kolejności tworzą ciąg geometryczny.
w podanej kolejności tworzą ciąg geometryczny.
Ramię trapezu równoramiennego ma długość 18 cm. Kąt rozwarty tego trapezu ma miarę dwa razy większą niż kąt ostry, a przekątna trapezu jest prostopadła do ramienia. Oblicz pole trapezu.

