/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki poziom rozszerzony CKE 3 kwietnia 2020 Czas pracy: 180 minut
Zadania zamknięte
Niech 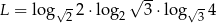 . Wtedy
. Wtedy
A) 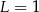 B)
B) 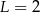 C)
C) 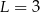 D)
D) 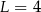
Okrąg o równaniu 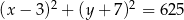 jest styczny do okręgu o środku
jest styczny do okręgu o środku 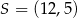 i promieniu
i promieniu  . Wynika stąd, że
. Wynika stąd, że
A) 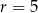 B)
B) 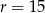 C)
C) 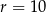 D)
D) 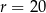
Liczba 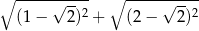 jest równa
jest równa
A) 1 B) 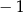 C)
C) 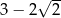 D)
D) 
Spośród poniższych nierówności wskaż tę, którą spełniają dokładnie trzy liczby całkowite.
A) 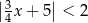 B)
B) 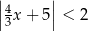 C)
C) 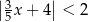 D)
D) 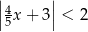
Zadania otwarte
Oblicz współczynnik kierunkowy stycznej do wykresu funkcji 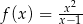 , określonej dla każdej liczby rzeczywistej
, określonej dla każdej liczby rzeczywistej 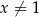 , poprowadzonej w punkcie
, poprowadzonej w punkcie 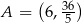 tego wykresu.
tego wykresu.
W trójkącie 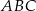 kąt
kąt 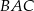 jest dwa razy większy od kąta
jest dwa razy większy od kąta 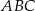 . Wykaż, że prawdziwa jest równość
. Wykaż, że prawdziwa jest równość 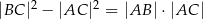 .
.
Udowodnij, że dla dowolnego kąta 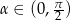 prawdziwa jest nierówność
prawdziwa jest nierówność
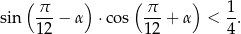
Wykaż, że równanie 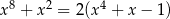 ma tylko jedno rozwiązanie rzeczywiste
ma tylko jedno rozwiązanie rzeczywiste 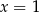 .
.
Ze zbioru wszystkich liczb naturalnych ośmiocyfrowych, w których zapisie dziesiętnym występują tylko cyfry ze zbioru 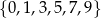 , losujemy jedną. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma cyfr wylosowanej liczby jest równa 3.
, losujemy jedną. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma cyfr wylosowanej liczby jest równa 3.
Dany jest rosnący ciąg geometryczny 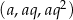 , którego wszystkie wyrazy i iloraz są liczbami całkowitymi nieparzystymi. Jeśli największy wyraz ciągu zmniejszymy o 4, to otrzymamy ciąg arytmetyczny. Oblicz wyraz
, którego wszystkie wyrazy i iloraz są liczbami całkowitymi nieparzystymi. Jeśli największy wyraz ciągu zmniejszymy o 4, to otrzymamy ciąg arytmetyczny. Oblicz wyraz 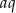 tego ciągu.
tego ciągu.
Dany jest nieskończony ciąg okręgów 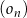 o równaniach
o równaniach 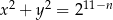 ,
, 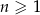 . Niech
. Niech 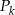 będzie pierścieniem ograniczonym zewnętrznym okręgiem
będzie pierścieniem ograniczonym zewnętrznym okręgiem 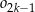 i wewnętrznym okręgiem
i wewnętrznym okręgiem 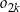 . Oblicz sumę pól wszystkich pierścieni
. Oblicz sumę pól wszystkich pierścieni 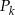 , gdzie
, gdzie 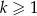 .
.
Trapez prostokątny 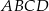 o podstawach
o podstawach 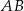 i
i 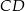 jest opisany na okręgu. Ramię
jest opisany na okręgu. Ramię 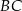 ma długość 10, a ramię
ma długość 10, a ramię 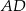 jest wysokością trapezu. Podstawa
jest wysokością trapezu. Podstawa 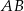 jest 2 razy dłuższa od podstawy
jest 2 razy dłuższa od podstawy 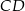 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Wierzchołki 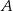 i
i 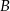 trójkąta prostokątnego
trójkąta prostokątnego 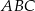 leżą na osi
leżą na osi 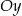 układu współrzędnych. Okrąg wpisany w ten trójkąt jest styczny do boków
układu współrzędnych. Okrąg wpisany w ten trójkąt jest styczny do boków 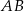 ,
, 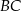 i
i 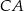 w punktach – odpowiednio –
w punktach – odpowiednio – 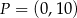 ,
, 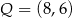 i
i 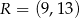 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 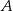 ,
, 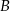 i
i 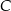 tego trójkąta.
tego trójkąta.
Wyznacz wszystkie wartości parametru 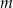 , dla których równanie
, dla których równanie
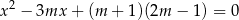
ma dwa różne rozwiązania 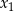 ,
, 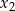 spełniające warunki:
spełniające warunki: 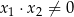 oraz
oraz 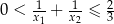 .
.
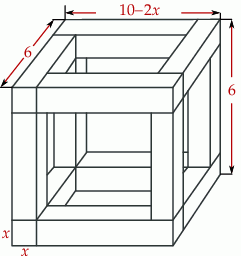
Rozpatrujemy wszystkie możliwe drewniane szkielety o kształcie przedstawionym na rysunku, wykonane z listewek. Każda z tych listewek ma kształt prostopadłościanu o podstawie kwadratu o boku długości  . Wymiary szkieletu zaznaczono na rysunku.
. Wymiary szkieletu zaznaczono na rysunku.
- Wyznacz objętość
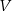 drewna potrzebnego do budowy szkieletu jako funkcję zmiennej
drewna potrzebnego do budowy szkieletu jako funkcję zmiennej  .
. - Wyznacz dziedzinę funkcji
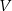 .
. - Oblicz tę wartość
 , dla której zbudowany szkielet jest możliwie najcięższy, czyli kiedy funkcja
, dla której zbudowany szkielet jest możliwie najcięższy, czyli kiedy funkcja 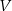 osiąga wartość największą. Oblicz tę największą objętość.
osiąga wartość największą. Oblicz tę największą objętość.

