/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 10 kwietnia 2021 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 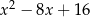 dla
dla 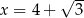 jest równa
jest równa
A) 3 B) 16 C) 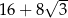 D)
D) 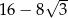
Wyrażenie 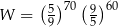 jest równe
jest równe
A) 1 B) 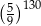 C)
C) 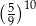 D)
D) 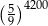
Liczba 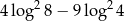 jest równa
jest równa
A) 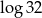 B)
B) 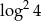 C)
C) 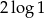 D)
D) 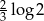
Badając pewien roztwór stwierdzono, że zawiera on 0,05 g chloru, co stanowi 0,01% masy roztworu. Jaka była masa roztworu?
A) 5 kg B) 50 g C) 500 g D) 5 g
Wskaż nierówność, której nie spełnia żadna liczba dodatnia.
A) 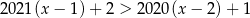 B)
B) 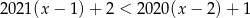
C) 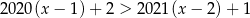 D)
D) 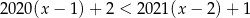
Kwotę 1000 zł wpłacamy do banku na 2 lata. Kapitalizacja odsetek jest dokonywana w tym banku co kwartał, a roczna stopa procentowa wynosi 5%. Po dwóch latach otrzymamy kwotę
A) 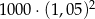 B)
B) 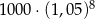 C)
C) 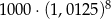 D)
D) 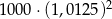
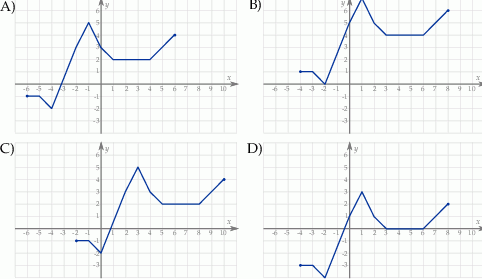
Rysunek przedstawia wykres funkcji 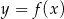 .
.
Wskaż wykres funkcji 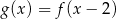 .
.
Dziedziną funkcji 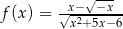 jest
jest
A) 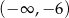 B)
B) 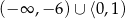 C)
C) 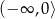 D)
D) 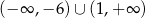
Osią symetrii wykresu funkcji kwadratowej 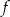 określonej wzorem
określonej wzorem 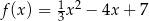 jest prosta o równaniu
jest prosta o równaniu
A) 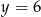 B)
B) 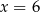 C)
C) 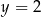 D)
D) 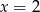
Funkcja 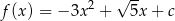 ma jedno miejsce zerowe. Zatem
ma jedno miejsce zerowe. Zatem
A) 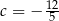 B)
B) 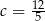 C)
C) 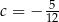 D)
D) 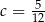
Na rysunku przedstawiono fragment wykresu funkcji liniowej 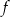 określonej wzorem
określonej wzorem 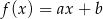 .
.
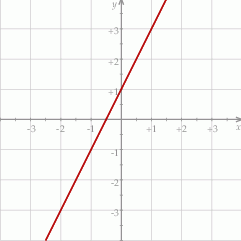
Współczynniki  oraz
oraz 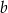 we wzorze funkcji
we wzorze funkcji 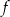 spełniają zależność
spełniają zależność
A) 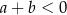 B)
B) 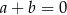 C)
C) 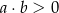 D)
D) 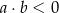
Równanie 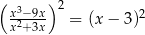
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma więcej niż dwa rozwiązania rzeczywiste.
Największą liczbą całkowitą spełniającą nierówność 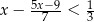 jest liczba
jest liczba
A) 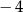 B)
B) 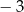 C) 2 D) 3
C) 2 D) 3
Jeśli trzeci wyraz ciągu geometrycznego jest równy 4, a czwarty wyraz tego ciągu jest równy 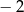 , to drugi wyraz jest równy
, to drugi wyraz jest równy
A) 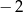 B) 2 C)
B) 2 C) 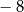 D) 8
D) 8
W ciągu arytmetycznym 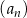 , określonym dla
, określonym dla 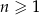 , szósty wyraz jest równy
, szósty wyraz jest równy 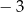 , a różnica tego ciągu jest równa 5. Suma
, a różnica tego ciągu jest równa 5. Suma 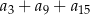 jest równa
jest równa
A) 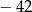 B)
B) 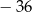 C) 36 D) 42
C) 36 D) 42
Przyprostokątna 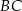 trójkąta prostokątnego
trójkąta prostokątnego 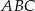 ma długość 6, a wysokość
ma długość 6, a wysokość 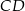 dzieli go na dwa takie trójkąty
dzieli go na dwa takie trójkąty 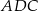 i
i 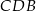 , że pole trójkąta
, że pole trójkąta 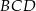 jest 4 razy mniejsze od pola trójkąta
jest 4 razy mniejsze od pola trójkąta 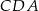 (zobacz rysunek).
(zobacz rysunek).
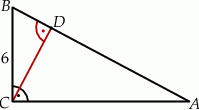
Przyprostokątna 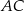 trójkąta prostokątnego
trójkąta prostokątnego 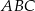 jest równa
jest równa
A) 12 B) 8 C) 9 D) 24
Miara kąta wpisanego opartego na łuku długości 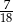 długości całego okręgu wynosi
długości całego okręgu wynosi
A) 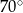 B)
B) 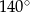 C)
C) 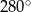 D)
D) 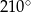
Funkcja 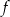 jest określona wzorem
jest określona wzorem 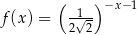 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych  . Funkcja
. Funkcja 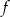 dla argumentu
dla argumentu 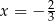 przyjmuje wartość
przyjmuje wartość
A) 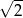 B)
B) 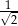 C)
C) 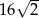 D)
D) 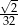
Dany jest trójkąt prostokątny o kątach ostrych  i
i 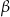 (zobacz rysunek).
(zobacz rysunek).
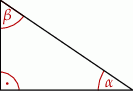
Wyrażenie 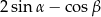 jest równe
jest równe
A) 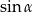 B)
B) 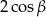 C) 0 D) 2
C) 0 D) 2
Dany jest trójkąt o wierzchołkach 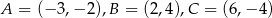 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 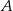 jest równa
jest równa
A) 4 B) 6 C) 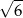 D)
D) 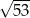
Punkty 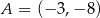 i
i 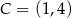 są wierzchołkami rombu
są wierzchołkami rombu 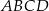 . Wierzchołki
. Wierzchołki  i
i  tego rombu są zawarte w prostej o równaniu
tego rombu są zawarte w prostej o równaniu 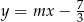 . Zatem
. Zatem
A) 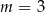 B)
B) 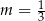 C)
C) 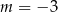 D)
D) 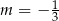
Punkt 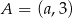 leży powyżej prostej określonej równaniem
leży powyżej prostej określonej równaniem 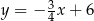 . Stąd wynika, że
. Stąd wynika, że
A) 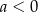 B)
B) 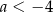 C)
C) 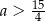 D)
D) 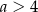
Sześć liczb: 19, 15, 13,  , 7, 1, tworzących zestaw danych, jest uporządkowanych malejąco. Mediana tego zestawu sześciu danych jest równa medianie zestawu pięciu danych: 15,
, 7, 1, tworzących zestaw danych, jest uporządkowanych malejąco. Mediana tego zestawu sześciu danych jest równa medianie zestawu pięciu danych: 15,  , 8, 2, 19. Zatem
, 8, 2, 19. Zatem
A) 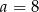 B)
B) 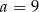 C)
C) 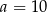 D)
D) 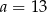
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2021 i podzielnych przez 3?
A) 673 B) 334 C) 340 D) 339
Prosta 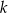 przecina oś
przecina oś 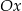 układu współrzędnych w punkcie
układu współrzędnych w punkcie 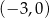 i jest równoległa do prostej o równaniu
i jest równoległa do prostej o równaniu 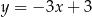 . Wówczas prosta
. Wówczas prosta 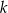 przecina oś
przecina oś 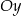 układu współrzędnych w punkcie
układu współrzędnych w punkcie
A) 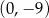 B)
B) 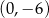 C)
C) 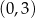 D)
D) 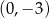
Ze zbioru trzycyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 15 jest równe
A) 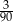 B)
B) 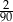 C)
C) 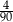 D)
D) 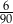
Liczba przekątnych graniastosłupa prawidłowego sześciokątnego jest równa
A) 12 B) 18 C) 6 D) 9
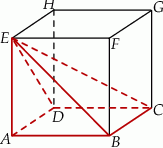
Dany jest sześcian  .
.
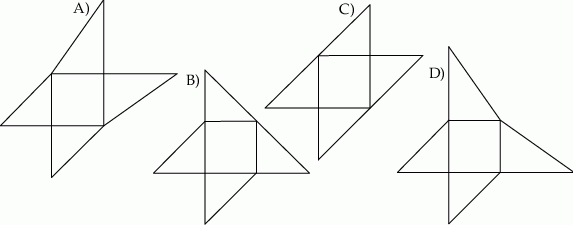
Siatką ostrosłupa czworokątnego  jest
jest
Zadania otwarte
Rozwiąż równanie 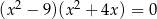 .
.
Kąt  spełnia warunek:
spełnia warunek: 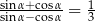 . Oblicz
. Oblicz 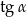 .
.
Dane są dwa przeciwległe wierzchołki kwadratu 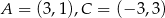 . Oblicz obwód tego kwadratu.
. Oblicz obwód tego kwadratu.
Wykaż, że dla dowolnych liczb rzeczywistych 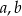 prawdziwa jest nierówność
prawdziwa jest nierówność
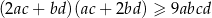
W pudełku jest 9 kul, z czego 7 białych i 2 czarne. Do tego pudełka dołożono  kul białych. Doświadczenie polega na losowaniu jednej kuli z tego pudełka. Prawdopodobieństwo, że będzie to kula biała, jest równe
kul białych. Doświadczenie polega na losowaniu jednej kuli z tego pudełka. Prawdopodobieństwo, że będzie to kula biała, jest równe 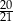 . Oblicz
. Oblicz  .
.
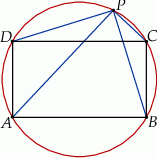
Punkt 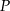 należy do okręgu opisanego na prostokącie
należy do okręgu opisanego na prostokącie 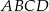 . Wykaż, że
. Wykaż, że 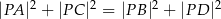 .
.
Dany jest romb 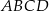 o boku długości 26, w którym przekątna
o boku długości 26, w którym przekątna 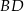 ma długość równą 20. Punkt
ma długość równą 20. Punkt 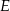 jest środkiem boku
jest środkiem boku 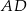 (zobacz rysunek).
(zobacz rysunek).
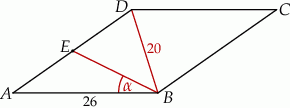
Oblicz sinus kąta  , jaki odcinek
, jaki odcinek 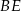 tworzy z bokiem
tworzy z bokiem 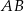 rombu
rombu 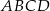 .
.

