/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 5 marca 2011 Czas pracy: 170 minut
Zadania zamknięte
Spodnie po obniżce ceny o 25% kosztują 168 zł. Ile kosztowały spodnie przed obniżką?
A) 193 zł B) 210 zł C) 224 zł D) 336 zł
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 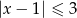 .
.

Trzecia część liczby 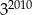 to
to
A) 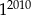 B)
B) 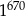 C)
C) 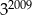 D)
D) 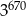
Funkcja liniowa 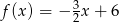 przyjmuje wartości ujemne dla:
przyjmuje wartości ujemne dla:
A) 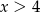 B)
B) 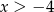 C)
C) 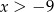 D)
D) 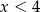
Rysunek przedstawia wykres funkcji 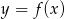 .
.
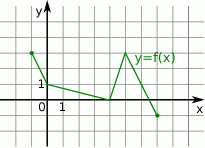
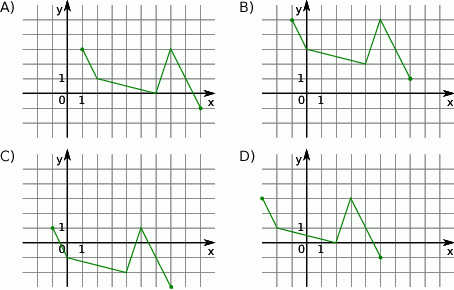
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 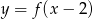 .
.
Liczba 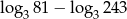 jest równa
jest równa
A) -2 B) -1 C) 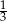 D) 3
D) 3
Największą liczbą naturalną, która nie spełnia nierówności 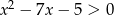 jest
jest
A) 0 B) 3 C) 7 D) 8
Równanie 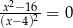
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma dokładnie cztery rozwiązania.
Wykresem funkcji kwadratowej 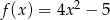 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie
A) 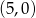 B)
B) 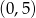 C)
C) 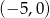 D)
D) 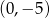
Liczba -1 jest miejscem zerowym funkcji liniowej 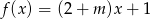 . Wynika stąd, że
. Wynika stąd, że
A) 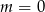 B)
B) 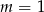 C)
C) 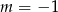 D)
D) 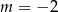
Wartość wyrażenia 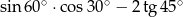 jest równa
jest równa
A) 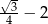 B)
B) 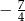 C)
C) 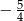 D)
D) 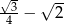
W ciągu geometrycznym 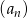 dane są:
dane są: 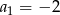 i
i 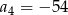 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 3 B) 27 C) 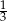 D)
D) 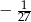
Do wykresu funkcji 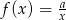 , dla
, dla 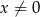 należy punkt
należy punkt 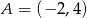 . Wtedy
. Wtedy
A) 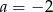 B)
B) 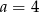 C)
C) 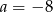 D)
D) 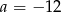
Liczby: 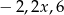 w podanej kolejności tworzą ciąg arytmetyczny. Zatem liczba
w podanej kolejności tworzą ciąg arytmetyczny. Zatem liczba  jest równa
jest równa
A) 4 B) 1 C) -1 D) 2
Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 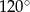 . Jaka jest miara kąta środkowego?
. Jaka jest miara kąta środkowego?
A) 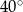 B)
B) 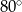 C)
C) 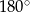 D)
D) 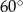
Jeżeli wysokość trójkąta równobocznego wynosi 4, to długość jego boku jest równa
A) 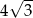 B)
B) 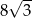 C)
C) 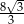 D) 12
D) 12
Długość odcinka  jest równa
jest równa
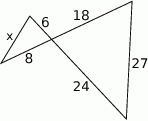
A) 9 B) 8 C) 12 D) 7,5
Przekątna 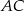 prostokąta
prostokąta 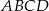 ma długość 13, a bok
ma długość 13, a bok 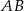 jest od niej o 5 krótszy. Oblicz długość boku
jest od niej o 5 krótszy. Oblicz długość boku 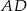 .
.
A)  B) 11 C)
B) 11 C) 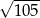 D)
D) 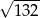
Wskaż równanie okręgu o promieniu 4.
A) 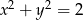 B)
B) 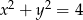 C)
C) 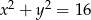 D)
D) 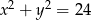
Kąt  jest ostry i
jest ostry i 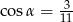 . Wówczas
. Wówczas 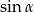 jest równy
jest równy
A) 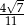 B)
B) 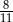 C)
C) 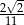 D)
D) 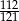
Punkty 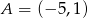 i
i 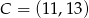 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 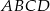 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 10 B) 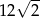 C) 20 D)
C) 20 D) 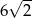
Suma długości wszystkich krawędzi sześcianu jest równa 24. Pole powierzchni tego sześcianu jest równe
A) 4 B) 16 C) 24 D) 8
Wybieramy liczbę  ze zbioru
ze zbioru 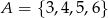 oraz liczbę
oraz liczbę 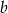 ze zbioru
ze zbioru 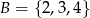 . Ile jest takich par
. Ile jest takich par 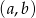 , że iloczyn
, że iloczyn 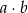 jest liczbą nieparzystą?
jest liczbą nieparzystą?
A) 12 B) 3 C) 2 D) 20
W czterech rzutach sześcienną kostką do gry otrzymano następujące liczby oczek: 6, 3, 1, 2. Mediana tych danych jest równa
A) 2 B) 2,5 C) 3 D) 3,5
Zadania otwarte
Rozwiąż nierówność: 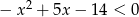 .
.
Proste o równaniach 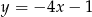 i
i 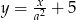 są prostopadłe. Wyznacz liczbę
są prostopadłe. Wyznacz liczbę  .
.
Siódmy wyraz ciągu arytmetycznego jest równy 34, a suma siedmiu początkowych wyrazów tego ciągu jest równa 56. Oblicz pierwszy wyraz tego ciągu.
Podaj przykład liczb całkowitych dodatnich, spełniających nierówność 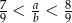 .
.
Dany jest trójkąt równoboczny 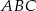 . Okrąg o średnicy
. Okrąg o średnicy 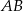 przecina bok
przecina bok 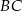 w punkcie
w punkcie 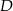 .
.
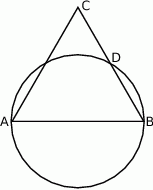
Wykaż, że 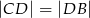 .
.
Wykaż, że jeżeli 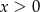 i
i 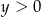 to
to 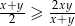 .
.
Podstawą ostrosłupa 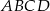 jest trójkąt
jest trójkąt 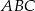 . Krawędź
. Krawędź 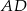 jest wysokością ostrosłupa (zobacz rysunek).
jest wysokością ostrosłupa (zobacz rysunek).
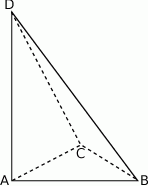
Oblicz objętość ostrosłupa 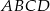 , jeśli wiadomo, że
, jeśli wiadomo, że 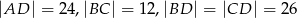 .
.
Pan Andrzej przeczytał książkę liczącą 720 stron, przy czym każdego dnia czytał taką samą liczbę stron. Gdyby czytał każdego dnia o 8 stron więcej to przeczytałby tę książkę o 15 dni wcześniej. Ile dni czytał tę książkę?
Wyznacz współrzędne punktu przecięcia przekątnych czworokąta 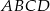 jeżeli
jeżeli 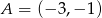 ,
, 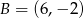 ,
, 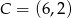 i
i 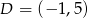 .
.

