/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom podstawowy 28 maja 2009 Czas pracy: 170 minut
Zadania zamknięte
Wykresem funkcji nie może być:
A) prosta B) punkt C) okrąg D) odcinek
Funkcja 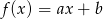 dla ujemnych argumentów przyjmuje wartości ujemne, a dla dodatnich argumentów wartości dodatnie. Wynika stąd, że:
dla ujemnych argumentów przyjmuje wartości ujemne, a dla dodatnich argumentów wartości dodatnie. Wynika stąd, że:
A) 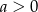 B)
B) 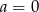 C)
C) 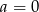 i
i 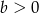 D)
D) 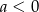
Do wykresu funkcji 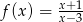 należy punkt
należy punkt
A) 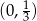 B)
B) 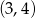 C)
C) 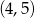 D)
D) 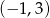
Dziedziną funkcji 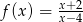 jest zbiór:
jest zbiór:
A) 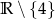 B)
B) 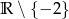 C)
C) 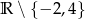 D)
D) 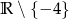
Zbiór liczb rzeczywistych jest dziedziną funkcji:
A) 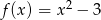 B)
B) 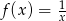 C)
C) 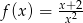 D)
D) 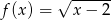
Jeśli towar kosztuje 241 zł 56 gr razem z 22% podatkiem VAT, to jego cena bez podatku jest równa:
A) 198 zł B) 180 zł C) 172 zł D) 157 zł 76 gr
Jeżeli 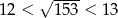 , to liczba
, to liczba 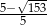 należy do przedziału:
należy do przedziału:
A) 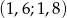 B)
B) 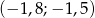 C)
C) 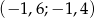 D)
D) 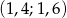
Kąty między bokiem trójkąta ostrokątnego a wysokościami opuszczonymi z należących do tego boku wierzchołków mają miary 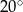 i
i 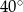 . Kąty tego trójkąta mają miary:
. Kąty tego trójkąta mają miary:
A) 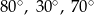 B)
B) 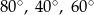 C)
C) 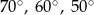 D)
D) 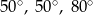
Trójkąt można zbudować z odcinków o długościach:
A) 10, 6, 5 B) 4, 2, 1 C) 8, 5, 3 D) 6, 6, 13
Prostą równoległą do prostej 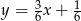 jest prosta:
jest prosta:
A) 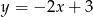 B)
B) 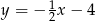 C)
C) 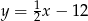 D)
D) 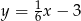
Jedna z przyprostokątnych trójkąta prostokątnego jest 3 razy dłuższa od drugiej. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 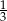 B) 3 C)
B) 3 C) 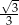 D)
D) 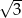
Przesuwając wykres funkcji 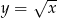 o dwie jednostki w górę otrzymujemy funkcję:
o dwie jednostki w górę otrzymujemy funkcję:
A) 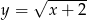 B)
B) 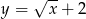 C)
C) 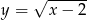 D)
D) 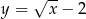
Określ liczbę miejsc zerowych funkcji:
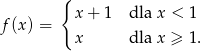
A) 0 B) 1 C) 2 D) 3
Miejscem zerowym funkcji 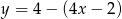 jest:
jest:
A) 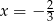 B)
B) 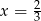 C)
C) 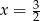 D)
D) 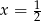
Ewa ma o 25% pieniędzy więcej niż Joasia. O ile procent Joasia ma mniej pieniędzy niż Ewa?
A) 25% B) 20% C) 50% D) 100%
Liczbą wymierną nie jest:
A) 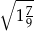 B)
B) 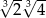 C)
C) 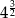 D)
D) 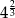
Przedział 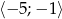 zapisany za pomocą wartości bezwzględnej to:
zapisany za pomocą wartości bezwzględnej to:
A) 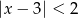 B)
B) 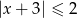 C)
C) 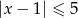 D)
D) 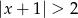
Prosta 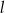 ma równanie
ma równanie 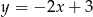 . Równaniem prostej prostopadłej do
. Równaniem prostej prostopadłej do 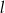 i przechodzącej przez punkt
i przechodzącej przez punkt 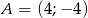 jest:
jest:
A) 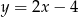 B)
B) 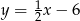 C)
C) 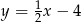 D)
D) 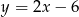
Odcinek o końcach 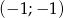 i
i 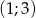 jest zawarty w prostej:
jest zawarty w prostej:
A) 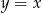 B)
B) 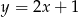 C)
C) 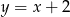 D)
D) 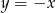
Dany jest układ równań: 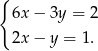 Prawdziwe jest zdanie:
Prawdziwe jest zdanie:
A) jednym z rozwiązań układu jest para liczb 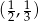
B) układ równań ma nieskończenie wiele rozwiązań
C) układ równań nie ma rozwiązań
D) układ równań ma dokładnie jedno rozwiązanie
Zadania otwarte
Oblicz błąd bezwzględny przybliżenia: 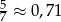 .
.
Wyznacz wzór funkcji liniowej o współczynniku kierunkowym 2 i przechodzącej przez punkt 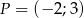 .
.
Sprawdź tożsamość: 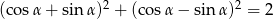 .
.
Oblicz wysokość prostopadłościanu, którego podstawa jest prostokątem o wymiarach 3 i 4, a pole powierzchni całkowitej wynosi 94.
Nachylenie stoku wynosi 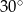 , a długość stoku 150 m. Podaj różnicę wzniesień.
, a długość stoku 150 m. Podaj różnicę wzniesień.
Wiedząc, że boki trójkąta prostokątnego mają długości: 20, 15, 25, wyznacz długość wysokości opuszczonej na przeciwprostokątną.
W trójkącie prostokątnym iloczyn sinusa jednego z kątów ostrych i tangensa drugiego kąta ostrego jest równy 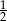 . Oblicz miary kątów ostrych tego trójkąta.
. Oblicz miary kątów ostrych tego trójkąta.
Wyznacz równanie symetralnej odcinka o końcach 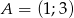 i
i 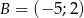 .
.
Wykaż, że dla dowolnej liczby całkowitej 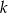 różnica iloczynu tej liczby i liczby od niej o 3 większej oraz iloczynu dwóch kolejnych liczb całkowitych większych od
różnica iloczynu tej liczby i liczby od niej o 3 większej oraz iloczynu dwóch kolejnych liczb całkowitych większych od 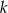 jest równa -2.
jest równa -2.
Z wierzchołków kwadratu o boku  , jako ze środków zakreślono 4 okręgi o promieniu
, jako ze środków zakreślono 4 okręgi o promieniu 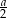 . Znajdź promienie okręgów stycznych do tych czterech okręgów jednocześnie.
. Znajdź promienie okręgów stycznych do tych czterech okręgów jednocześnie.
Wykres funkcji 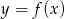 przesunięto równolegle do osi
przesunięto równolegle do osi 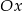 o 5 jednostek w prawo i równolegle do osi
o 5 jednostek w prawo i równolegle do osi 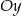 o 2 jednostki w dół. Podaj wzór funkcji:
o 2 jednostki w dół. Podaj wzór funkcji: 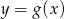 będącej obrazem wykresu funkcji
będącej obrazem wykresu funkcji 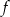 w przesunięciu, jeżeli
w przesunięciu, jeżeli 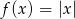 . Narysuj wykres funkcji
. Narysuj wykres funkcji 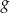 .
.
Średnica 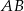 i cięciwa
i cięciwa 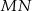 okręgu przecinają się w punkcie
okręgu przecinają się w punkcie 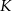 . Kąt
. Kąt 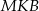 ma miarę
ma miarę 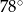 , a kąt środkowy oparty na łuku
, a kąt środkowy oparty na łuku 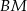 ma miarę
ma miarę 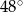 . Wyznacz miarę kąta
. Wyznacz miarę kąta 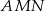 .
.

