/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 9 maja 2009 Czas pracy: 120 minut
Janek przez 4 miesiące odkładał pieniądze na zakup roweru. W pierwszym miesiącu odłożył 30% potrzebnej kwoty, w drugim miesiącu o 60 zł mniej niż w pierwszym, w trzecim połowę wciąż brakującej sumy, a w czwartym 270 zł. Oblicz jaka była cena roweru.
Oblicz 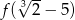 jeżeli
jeżeli 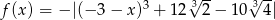 .
.
W równoległoboku 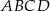 , w którym
, w którym 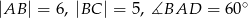 poprowadzono wysokości
poprowadzono wysokości 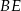 i
i 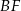 na boki
na boki 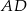 i
i 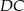 .
.
- Wykonaj odpowiedni rysunek i oblicz długości odcinków
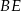 i
i 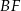 .
. - Oblicz pole trójkąta
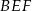 .
.
Paweł i Gaweł wyruszyli w 500 kilometrową podróż dwoma samochodami. Samochód Pawła poruszał się cały czas ze stałą prędkością, a sposób poruszania się samochodu Gawła przedstawiony jest na poniższym wykresie.
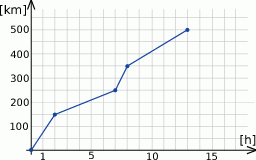
- Oblicz z jaką prędkością poruszał się samochód Pawła, jeżeli dojechał on do celu 20 minut po Gawle. Wynik podaj w kilometrach na godzinę
- Przez ile godzin Gaweł jechał wolniej od Pawła?
- Ile razy, i w której minucie podróży oba samochody się spotkały (nie licząc początku i końca podróży). Wynik podaj z dokładnością do 1 minuty.
W pojemniku znajduje się 28 kul, przy czym  z nich to kule białe, a pozostałe to kule czarne. Z pojemnika losujemy dwa razy po jednej kuli ze zwracaniem. Dla jakiej liczby
z nich to kule białe, a pozostałe to kule czarne. Z pojemnika losujemy dwa razy po jednej kuli ze zwracaniem. Dla jakiej liczby  prawdopodobieństwo wylosowania jednej kuli białej i jednej czarnej jest największe?
prawdopodobieństwo wylosowania jednej kuli białej i jednej czarnej jest największe?
Uzasadnij, że koło o środku 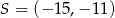 i promieniu
i promieniu 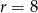 jest w całości zawarte w trójkącie o wierzchołkach
jest w całości zawarte w trójkącie o wierzchołkach 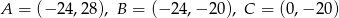 .
.
Wyznacz największą liczbę całkowitą spełniającą nierówność
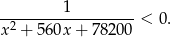
W fabryce zabawek znajduje się 10 maszyn do produkcji plastikowych samochodów. Średnia wydajność jednej maszyny wynosi 2100 samochodów dziennie. W okresie przedświątecznym uruchomiono jedną dodatkową maszynę, w wyniku czego średnia dzienna wydajność pojedynczego urządzenia zmalała o 4%. Oblicz ile samochodów dziennie produkuje dodatkowa maszyna.
Przekątna prostopadłościanu ma długość 5 i tworzy z dwoma ścianami prostopadłościanu kąty  i
i 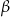 takie, że
takie, że 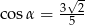 i
i 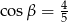 . Oblicz objętość tego prostopadłościanu.
. Oblicz objętość tego prostopadłościanu.
Wyznacz punkty wspólne wykresów funkcji 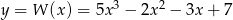 oraz
oraz 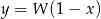 .
.
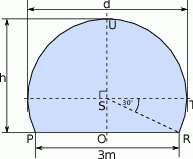
W architekturze islamu często stosowanym elementem był łuk podkowiasty. Schemat okna w kształcie takiego łuku (łuku okręgu) przedstawiono na rysunku poniżej. Korzystając z danych na rysunku oblicz wysokość okna 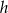 i największy prześwit
i największy prześwit 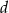 .
.
Klient zaciągnął w banku pożyczkę w wysokości 7200 zł. Spłatę rozłożył na 10 rat, z których każda następna jest mniejsza od poprzedniej o 60 zł. Oblicz sumę pierwszych pięciu rat.

