/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony
(technikum) 21 marca 2015 Czas pracy: 180 minut

Zadanie 1
(5 pkt)

Narysuj w układzie współrzędnych zbiór

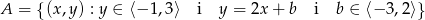
A = {(x,y) : y ∈ ⟨− 1,3 ⟩ i y = 2x + b i b ∈ ⟨− 3,2⟩}

oraz oblicz jego pole powierzchni.

Zadanie 2
(4 pkt)

Wyznacz te wartości parametru 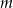m , dla których równanie

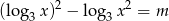
2 2 (log 3x) − log3x = m

ma dwa rozwiązania należące do przedziału 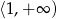⟨1,+ ∞ ) .

Zadanie 3
(4 pkt)

Punkt 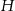H jest punktem wspólnym wysokości trójkąta ostrokątnego 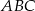ABC wpisanego w okrąg o promieniu 12. Oblicz promień okręgu opisanego na trójkącie ABH .

Zadanie 4
(4 pkt)

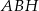Rozwiąż równanie 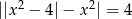2 2 ||x − 4|− x | = 4 .

Zadanie 5
(4 pkt)

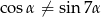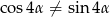Udowodnij, że jeżeli cosα ⁄= sin 7α i cos4 α ⁄= sin4 α to

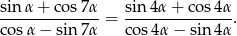
sin α + co s7α sin4α + co s4α --------------= ---------------. cosα − sin 7α cos 4α− sin 4α

Zadanie 6
(4 pkt)

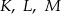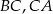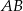Punkty K, L, M są środkami boków BC ,CA i AB trójkąta 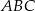ABC . Wykaż, że

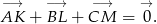
− → − → −→ → AK + BL + CM = 0.

Zadanie 7
(5 pkt)

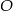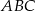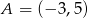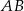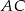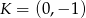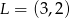Okrąg o środku O jest wpisany w trójkąt ABC , gdzie A = (− 3,5) . Wiedząc, że okrąg ten jest styczny do boków AB i AC odpowiednio w punktach K = (0,− 1) i L = (3 ,2) oblicz długość odcinka AO .

Zadanie 8
(5 pkt)

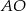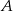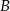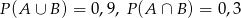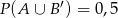O zdarzeniach losowych A i B wiadomo, że P(A ∪ B) = 0,9 , P (A ∩ B) = 0,3 i ′ P(A ∪ B ) = 0,5 . Oblicz ′ P (A ∪ B) .

Zadanie 9
(3 pkt)

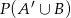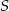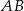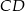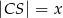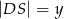Przez środek S cięciwy AB okręgu poprowadzono cięciwę CD , przy czym |CS | = x i |DS | = y . Oblicz długość cięciwy AB .

Zadanie 10
(4 pkt)

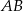Udowodnij, że suma sześcianów trzech kolejnych liczb naturalnych jest podzielna przez 9.

Zadanie 11
(4 pkt)

Dane są punkty 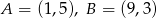A = (1,5), B = (9,3) i prosta 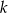k o równaniu 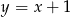y = x + 1 . Oblicz współrzędne punktu 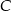C leżącego na prostej 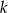k , dla którego suma 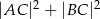|AC |2 + |BC |2 jest najmniejsza.

Zadanie 12
(4 pkt)

Stosunek pola powierzchni bocznej stożka do pola przekroju osiowego tego stożka jest równy √2π- 3 . Oblicz kąt rozwarcia stożka.

Arkusz Wersja PDF
Rozwiązania