/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki (CEN Bydgoszcz)
poziom podstawowy 5 marca 2020 Czas pracy: 170 minut
Zadania zamknięte
Zysk ze sprzedaży towaru w pewnej hurtowni w pierwszym miesiącu był równy 5000 zł, a w każdym następnym miesiącu o 5% wyższy w stosunku do miesiąca poprzedniego. Zysk hurtowni w szóstym miesiącu jej działalności opisuje wzór
A) 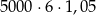 B)
B) 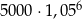 C)
C) 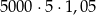 D)
D) 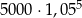
Liczba 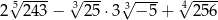 jest równa
jest równa
A) 25 B) 15 C) 12 D) 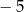
Wartość wyrażenia 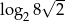 jest równa
jest równa
A)  B)
B)  C)
C) 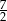 D)
D) 
Wyrażenie 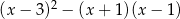 można przedstawić w postaci
można przedstawić w postaci
A) 8 B) 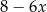 C) 10 D)
C) 10 D) 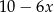
Najmniejszą liczbą całkowitą spełniającą nierówność 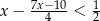 jest liczba
jest liczba
A) 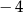 B)
B) 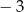 C) 2 D) 3
C) 2 D) 3
Równanie 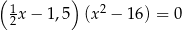
A) ma trzy różne rozwiązania B) ma dwa różne rozwiązania
C) ma jedno rozwiązanie D) nie ma rozwiązań
Na rysunku poniżej przedstawiony jest wykres funkcji 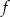 .
.
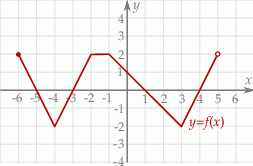
Funkcja ta przyjmuje wartości nieujemne dla
A) 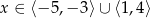 B)
B) 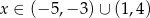
C) 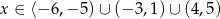 D)
D) 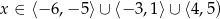
Wykres funkcji 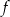 przedstawionej na rysunku powstał przez przesunięcie wykresu funkcji
przedstawionej na rysunku powstał przez przesunięcie wykresu funkcji 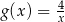 wzdłuż osi odciętych.
wzdłuż osi odciętych.
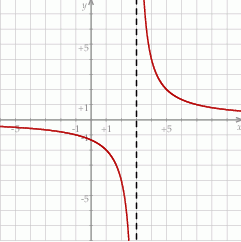
Funkcja 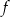 jest określona wzorem
jest określona wzorem
A) 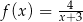 B)
B) 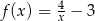 C)
C) 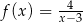 D)
D) 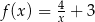
Funkcja liniowa 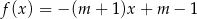 jest rosnąca dla
jest rosnąca dla
A) 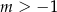 B)
B) 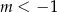 C)
C) 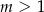 D)
D) 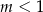
Wykres funkcji liniowej 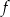 jest nachylony do osi
jest nachylony do osi 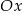 pod kątem
pod kątem 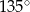 . Wiadomo, że
. Wiadomo, że 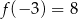 . Funkcja liniowa
. Funkcja liniowa 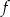 jest określona wzorem
jest określona wzorem
A) 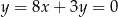 B)
B) 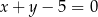
C) 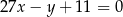 D)
D) 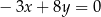
Proste 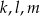 dane są równaniami
dane są równaniami 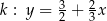 ,
, 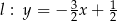 ,
, 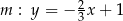 . Wynika stąd, że
. Wynika stąd, że
A) proste 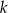 i
i 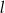 są prostopadłe
są prostopadłe
B) proste 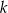 i
i 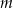 są prostopadłe
są prostopadłe
C) proste 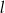 i
i 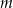 są prostopadłe
są prostopadłe
D) wśród prostych 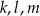 nie ma prostych prostopadłych
nie ma prostych prostopadłych
Punkt 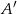 jest obrazem punktu
jest obrazem punktu 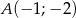 w symetrii względem prostej
w symetrii względem prostej 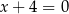 . Zatem
. Zatem
A) 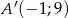 B)
B) 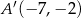 C)
C) 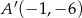 D)
D) 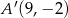
Punkt 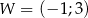 jest wierzchołkiem wykresu funkcji kwadratowej
jest wierzchołkiem wykresu funkcji kwadratowej 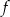 . Wobec tego funkcję
. Wobec tego funkcję 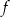 może przedstawiać wzór
może przedstawiać wzór
A) 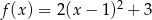 B)
B) 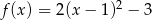
C) 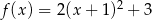 D)
D) 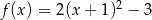
Dany jest ciąg 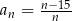 . Liczba całkowitych wyrazów tego ciągu jest równa
. Liczba całkowitych wyrazów tego ciągu jest równa
A) 0 B) 1 C) 3 D) 4
Liczby 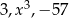 tworzą w podanej kolejności ciąg arytmetyczny. Liczba
tworzą w podanej kolejności ciąg arytmetyczny. Liczba  jest równa
jest równa
A) 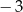 B) 3 C)
B) 3 C) 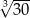 D)
D) 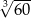
W rosnącym ciągu geometrycznym 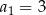 oraz
oraz 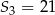 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 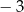 B)
B) 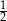 C) 2 D) 3
C) 2 D) 3
Liczba 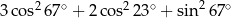 jest równa
jest równa
A) 3 B) 1 C) 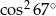 D)
D) 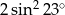
Dany jest trójkąt prostokątny o bokach długości 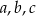 .
.
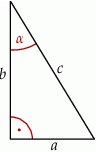
Jeżeli 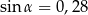 oraz
oraz 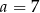 , to
, to
A) 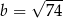 B)
B) 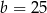 C)
C) 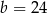 D)
D) 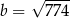
Okręgi o promieniach 4 cm oraz 6 cm są styczne zewnętrznie. Prosta, która jest styczna do okręgu o promieniu 6 cm w punkcie 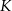 przechodzi przez środek okręgu o promieniu 4 cm (patrz rysunek).
przechodzi przez środek okręgu o promieniu 4 cm (patrz rysunek).
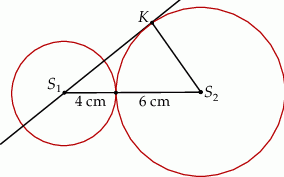
Długość odcinka 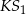 jest równa
jest równa
A) 6 cm B) 8 cm C) 10 cm D) 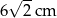
Pole rombu o boku 6 i kącie rozwartym 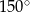 jest równe
jest równe
A) 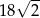 B) 18 C)
B) 18 C) 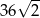 D) 36
D) 36
Punkt 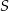 jest środkiem okręgu.
jest środkiem okręgu.
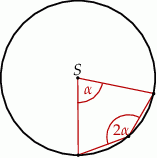
Miara kąta środkowego  jest równa
jest równa
A) 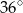 B)
B) 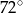 C)
C) 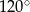 D)
D) 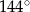
Powierzchnia boczna stożka o promieniu podstawy 6 cm, po rozwinięciu jest wycinkiem koła o kącie 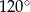 . Pole powierzchni bocznej tego stożka jest równe
. Pole powierzchni bocznej tego stożka jest równe
A) 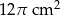 B)
B) 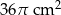 C)
C) 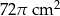 D)
D) 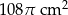
Pewien graniastosłup ma 57 krawędzi. Liczba wszystkich ścian tego graniastosłupa jest równa
A) 19 B) 21 C) 38 D) 57
Na diagramie przestawiono wzrost pięciorga uczniów.
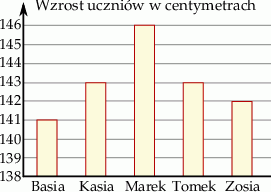
Odchylenie standardowe zestawu danych jest równe
A) 2 cm B) 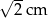 C)
C) 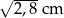 D) 2,8 cm
D) 2,8 cm
Z cyfr 1, 2, 3, 4, 5, 6 tworzymy sześciocyfrowe liczby o niepowtarzających się cyfrach w taki sposób, że cyfry parzyste zapisane są obok siebie. Powstało w ten sposób
A) 36 liczb B) 132 liczby C) 144 liczby D) 720 liczb
Zadania otwarte
Rozwiąż nierówność: 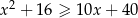 .
.
Udowodnij, że dla każdej liczby naturalnej  , gdzie
, gdzie 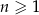 , liczba
, liczba 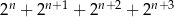 jest podzielna przez 30.
jest podzielna przez 30.
Liczebność kolonii bakterii pewnego szczepu w zależności od czasu opisuje funkcja 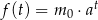 , gdzie
, gdzie 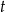 – oznacza czas obserwacji w godzinach,
– oznacza czas obserwacji w godzinach,  – pewną stałą dodatnią, a
– pewną stałą dodatnią, a 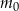 – liczebność początkowej próby bakterii. Na początku doświadczenia zaobserwowano 300 sztuk bakterii. Po dwóch godzinach liczba bakterii wzrosła do 1200. Po jakim czasie liczba bakterii wzrośnie do 153600?
– liczebność początkowej próby bakterii. Na początku doświadczenia zaobserwowano 300 sztuk bakterii. Po dwóch godzinach liczba bakterii wzrosła do 1200. Po jakim czasie liczba bakterii wzrośnie do 153600?
Pole kwadratu 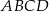 jest równe 16. Punkt
jest równe 16. Punkt 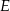 jest środkiem boku
jest środkiem boku 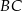 , a punkt
, a punkt 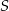 punktem przecięcia przekątnej
punktem przecięcia przekątnej 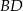 kwadratu i odcinka
kwadratu i odcinka 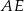 . Wykaż, że odległość punktu
. Wykaż, że odległość punktu 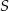 od boku
od boku 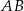 jest równa
jest równa 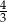 .
.
Na sześciu jednakowych kartkach napisano liczby: 1, 10, 100, 1000, 10000, 100000. Z tych kartek losujemy kolejno bez zwracania trzy. Oblicz prawdopodobieństwo, że suma wylosowanych liczb tworzy liczbę podzielną przez cztery.
W ciągu arytmetycznym 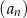 , dla
, dla 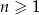 suma wyrazów trzeciego, czwartego i piątego wynosi 144. Oblicz sumę siedmiu początkowych wyrazów ciągu
suma wyrazów trzeciego, czwartego i piątego wynosi 144. Oblicz sumę siedmiu początkowych wyrazów ciągu 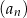 .
.
W trójkącie rozwartokątnym 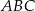 o kącie rozwartym przy wierzchołku
o kącie rozwartym przy wierzchołku 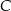 poprowadzono wysokość
poprowadzono wysokość 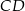 i otrzymano równoramienny trójkąt
i otrzymano równoramienny trójkąt 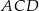 . Długości boków
. Długości boków 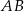 i
i 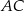 są odpowiednio równe
są odpowiednio równe 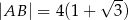 i
i 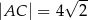 . Oblicz pole powierzchni koła opisanego na trójkącie
. Oblicz pole powierzchni koła opisanego na trójkącie 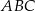 .
.
Właściciel sklepu kupuje zegarki płacąc producentowi 180 zł za sztukę. Następnie sprzedaje miesięcznie 30 sztuk takich zegarków po 230 zł. Sprzedawca oszacował, że każda obniżka ceny zegarka o złotówkę zwiększy liczbę sprzedanych zegarków o trzy sztuki. Niech  oznacza liczbę obniżek o 1 zł, gdzie
oznacza liczbę obniżek o 1 zł, gdzie 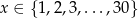 .
.
- Wyznacz wzór funkcji miesięcznego zysku właściciela sklepu w zależności od
 .
. - Jaką cenę zegarka powinien ustalić właściciel sklepu, aby jego miesięczny zysk był największy? Ile będzie równy ten największy miesięczny zysk?
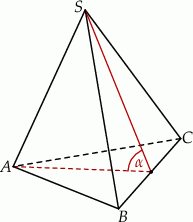
Pole podstawy ostrosłupa prawidłowego trójkątnego jest równe 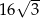 , a jego objętość
, a jego objętość 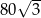 . Wyznacz cosinus kąta
. Wyznacz cosinus kąta  nachylenia ściany bocznej do płaszczyzny podstawy.
nachylenia ściany bocznej do płaszczyzny podstawy.