/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 8 marca 2014 Czas pracy: 180 minut

Zadanie 1
(4 pkt)

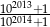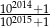Która z liczb jest większa: 102013+1 102014+1 , czy 102014+ 1 102015+-1 ?

Zadanie 2
(5 pkt)

Na rysunku przedstawiony jest fragment wykresu funkcji określonej wzorem 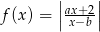|| || f (x) = |axx−+b2| .

PIC

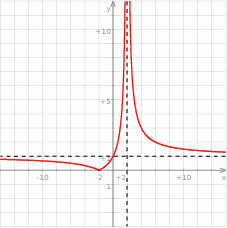
  • Oblicz a i b .
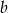  • Narysuj wykres funkcji określonej wzorem y = f (|x |) .
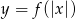  • Podaj wszystkie wartości parametru 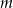m , dla których równanie 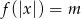f(|x|) = m ma cztery rozwiązania.

Zadanie 3
(5 pkt)

Na okręgu opisano trapez, w którym krótsza podstawa ma długość a , a dłuższa podstawa tworzy z ramionami kąty o mierze α . Oblicz pole tego trapezu.

Zadanie 4
(4 pkt)

Wykaż, że

∘ x ∘ x sin(30--+-2-)sin(30--−-2)- 2-cosx-−-1- cos(30∘ + x )cos(30∘ − x ) = 2 cosx + 1 . 2 2

Zadanie 5
(4 pkt)

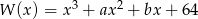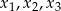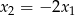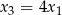Wielomian W (x) = x3 + ax2 + bx + 64 ma trzy pierwiastki: x1,x2,x 3 , przy czym x2 = − 2x 1 i x = 4x 3 1 . Wyznacz a i b .

Zadanie 6
(5 pkt)

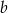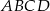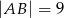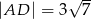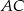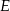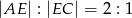W prostokącie ABCD , w którym |AB | = 9 , √ -- |AD | = 3 7 , na przekątnej AC wybrano taki punkt E , że |AE | : |EC | = 2 : 1 . Oblicz sinus kąta ∡EBC .

Zadanie 7
(6 pkt)

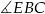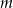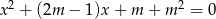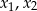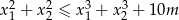Wyznacz wszystkie wartości parametru m , dla których równanie 2 2 x + (2m − 1)x + m + m = 0 ma dwa różne rozwiązania rzeczywiste x1,x2 spełniające warunek: x12+ x 22 ≤ x31 + x32 + 10m .

Zadanie 8
(6 pkt)

Punkt 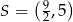(9 ) S = 2,5 jest środkiem symetrii prostokąta 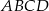ABCD , którego pole jest równe 30, a bok 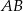AB jest zawarty w prostej o równaniu 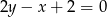2y − x + 2 = 0 . Oblicz współrzędne wierzchołków prostokąta ABCD .

Zadanie 9
(4 pkt)

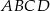Oblicz, ile jest liczb naturalnych czterocyfrowych takich, że iloczyn cyfr w ich zapisie dziesiętnym jest równy 36.

Zadanie 10
(4 pkt)

Suma krawędzi graniastosłupa prawidłowego trójkątnego jest równa 3. Dla jakiej długości krawędzi podstawy pole powierzchni całkowitej tego graniastosłupa będzie największe?

Zadanie 11
(3 pkt)

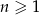Suma n ≥ 1 początkowych wyrazów ciągu 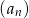(an) wyraża się wzorem 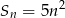2 Sn = 5n . Oblicz, ile wyrazów tego ciągu jest liczbami trzycyfrowymi.

Arkusz Wersja PDF
Rozwiązania