/Szkoła średnia/Zadania maturalne
Poprawkowy Egzamin Maturalny
z Matematyki poziom podstawowy 24 sierpnia 2021 Czas pracy: 170 minut
Zadania zamknięte
Liczba 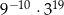 jest równa
jest równa
A) 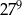 B)
B) 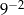 C)
C) 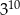 D)
D) 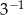
Liczba 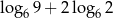 jest równa
jest równa
A) 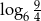 B) 1 C) 2 D)
B) 1 C) 2 D) 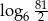
Liczba  stanowi 80% liczby dodatniej
stanowi 80% liczby dodatniej 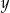 . Wynika stąd, że liczba
. Wynika stąd, że liczba 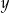 to
to
A) 125% liczby  B) 120% liczby
B) 120% liczby  C) 25% liczby
C) 25% liczby  D) 20% liczby
D) 20% liczby 
Dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 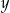 wyrażenie
wyrażenie 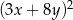 jest równe
jest równe
A) 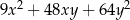 B)
B) 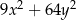 C)
C) 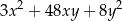 D)
D) 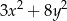
Liczba 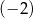 jest rozwiązaniem równania
jest rozwiązaniem równania
A) 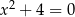 B)
B) 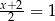 C)
C) 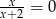 D)
D) 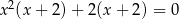
Zbiorem wszystkich rozwiązań nierówności 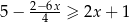 jest przedział
jest przedział
A) 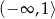 B)
B) 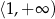 C)
C) 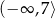 D)
D) 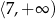
Funkcja liniowa 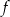 jest określona wzorem
jest określona wzorem 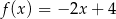 . Wykres funkcji
. Wykres funkcji 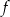 przesunięto wzdłuż osi
przesunięto wzdłuż osi 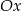 o 2 jednostki w lewo (tzn. przeciwnie do zwrotu osi), w wyniku czego otrzymano wykres funkcji
o 2 jednostki w lewo (tzn. przeciwnie do zwrotu osi), w wyniku czego otrzymano wykres funkcji 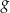 . Funkcja
. Funkcja 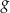 jest określona wzorem
jest określona wzorem
A) 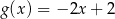 B)
B) 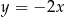 C)
C) 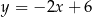 D)
D) 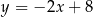
Funkcja 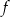 jest określona wzorem
jest określona wzorem 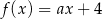 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba 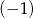 . Wtedy
. Wtedy
A) 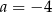 B)
B) 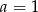 C)
C) 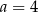 D)
D) 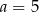
Prosta 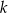 przechodzi przez punkt
przechodzi przez punkt 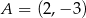 i jest nachylona do osi
i jest nachylona do osi 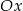 pod kątem
pod kątem 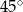 (zobacz rysunek).
(zobacz rysunek).
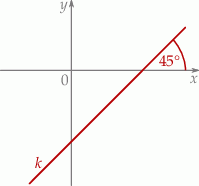
Prosta 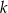 ma równanie
ma równanie
A) 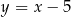 B)
B) 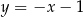 C)
C) 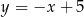 D)
D) 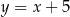
Funkcja kwadratowa 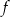 jest określona wzorem
jest określona wzorem 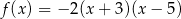 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 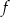 , ma współrzędną
, ma współrzędną  równą
równą
A) 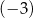 B)
B) 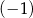 C) 1 D) 5
C) 1 D) 5
Funkcja 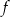 jest określona wzorem
jest określona wzorem 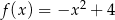 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Zbiorem wartości funkcji
. Zbiorem wartości funkcji 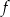 jest przedział
jest przedział
A) 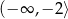 B)
B) 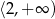 C)
C) 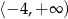 D)
D) 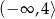
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 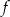 .
.
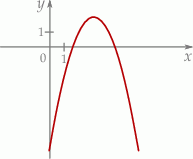
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 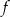 . A)
. A) 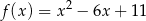 B)
B) 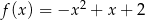
C) 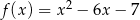 D)
D) 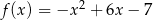
Ciąg arytmetyczny 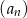 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 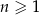 . Różnica tego ciągu jest równa 2. Wtedy
. Różnica tego ciągu jest równa 2. Wtedy
A) 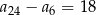 B)
B) 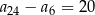 C)
C) 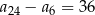 D)
D) 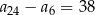
Suma wszystkich liczb całkowitych dodatnich parzystych i jednocześnie mniejszych od 1001 jest równa
A) 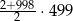 B)
B) 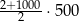 C)
C) 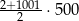 D)
D) 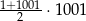
Trójwyrazowy ciąg 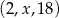 jest rosnącym ciągiem geometrycznym. Wtedy
jest rosnącym ciągiem geometrycznym. Wtedy
A) 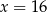 B)
B) 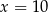 C)
C) 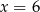 D)
D) 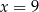
Kąt  jest ostry i
jest ostry i 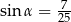 . Wynika stąd, że
. Wynika stąd, że
A) 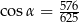 B)
B) 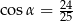 C)
C) 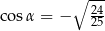 D)
D) 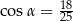
Czworokąt 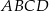 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 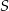 . Bok
. Bok 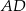 jest średnicą tego okręgu, a miara kąta
jest średnicą tego okręgu, a miara kąta 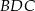 jest równa
jest równa 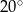 (zobacz rysunek).
(zobacz rysunek).
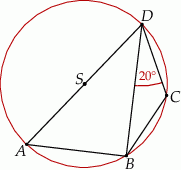
Wtedy miara kąta 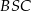 jest równa
jest równa
A) 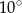 B)
B) 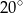 C)
C) 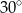 D)
D) 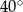
Okrąg o środku w punkcie 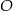 jest wpisany w trójkąt
jest wpisany w trójkąt 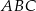 . Wiadomo, że
. Wiadomo, że 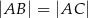 i
i 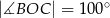 (zobacz rysunek).
(zobacz rysunek).
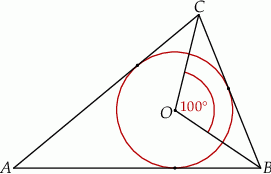
Miara kąta 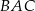 jest równa
jest równa
A) 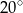 B)
B) 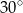 C)
C) 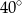 D)
D) 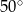
Punkty 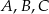 i
i 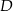 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 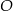 . Cięciwy
. Cięciwy 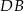 i
i 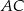 przecinają się w punkcie
przecinają się w punkcie 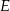 ,
, 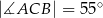 oraz
oraz 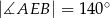 (zobacz rysunek).
(zobacz rysunek).
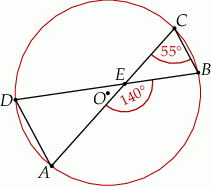
Miara kąta 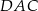 jest równa
jest równa
A) 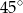 B)
B) 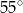 C)
C) 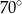 D)
D) 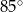
Przekątna 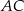 prostokąta
prostokąta 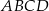 ma długość 70. Na boku
ma długość 70. Na boku 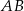 obrano punkt
obrano punkt 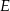 , na przekątnej
, na przekątnej 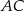 obrano punkt
obrano punkt 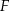 , a na boku
, a na boku 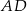 obrano punkt
obrano punkt 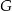 – tak, że czworokąt
– tak, że czworokąt 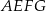 jest prostokątem (zobacz rysunek). Ponadto
jest prostokątem (zobacz rysunek). Ponadto 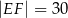 i
i 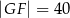 .
.
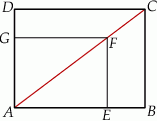
Obwód prostokąta 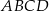 jest równy
jest równy
A) 158 B) 196 C) 336 D) 490
W układzie współrzędnych dane są dwa punkty 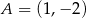 oraz
oraz 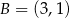 . Współczynnik kierunkowy prostej
. Współczynnik kierunkowy prostej 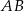 jest równy
jest równy
A) 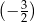 B)
B) 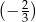 C)
C)  D)
D) 
Prosta 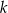 ma równanie
ma równanie 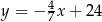 . Współczynnik kierunkowy prostej prostopadłej do prostej
. Współczynnik kierunkowy prostej prostopadłej do prostej 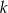 jest równy
jest równy
A)  B)
B) 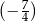 C)
C) 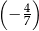 D)
D) 
Punkty 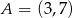 i
i 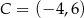 są końcami przekątnej kwadratu
są końcami przekątnej kwadratu 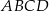 . Promień okręgu opisanego na tym kwadracie jest równy
. Promień okręgu opisanego na tym kwadracie jest równy
A) 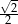 B)
B)  C)
C) 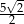 D) 5
D) 5
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 2 (zobacz rysunek).
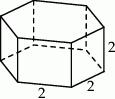
Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 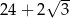 B)
B) 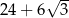 C)
C) 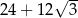 D)
D) 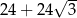
Przekątna sześcianu jest równa 6. Wynika stąd, że objętość tego sześcianu jest równa
A) 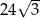 B) 72 C)
B) 72 C) 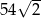 D)
D) 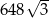
Wszystkich liczb naturalnych pięciocyfrowych parzystych jest
A) 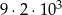 B)
B) 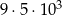 C)
C) 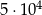 D)
D) 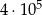
W pudełku znajdują się tylko kule białe i kule czerwone. Stosunek liczby kul białych do liczby kul czerwonych jest równy 3:4. Wylosowanie każdej kuli z tego pudełka jest jednakowo prawdopodobne. Losujemy jedną kulę. Niech 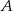 oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia 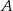 jest równe
jest równe
A) 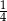 B)
B) 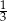 C)
C) 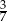 D)
D) 
Średnia arytmetyczna pięciu liczb: 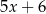 ,
, 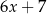 ,
, 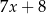 ,
, 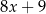 ,
, 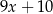 , jest równa 8. Wtedy
, jest równa 8. Wtedy  jest równe
jest równe
A) 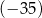 B) 0 C) 0,35 D) 35
B) 0 C) 0,35 D) 35
Zadania otwarte
Rozwiąż nierówność 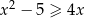 .
.
Rozwiąż równanie 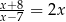 .
.
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 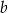 spełniona jest nierówność
spełniona jest nierówność
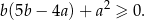
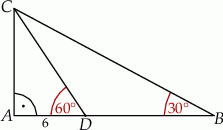
W trójkącie 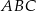 kąt przy wierzchołku
kąt przy wierzchołku 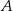 jest prosty, a kąt przy wierzchołku
jest prosty, a kąt przy wierzchołku 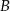 ma miarę
ma miarę 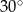 . Na boku
. Na boku 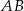 tego trójkąta obrano punkt
tego trójkąta obrano punkt 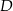 tak, że miara kąta
tak, że miara kąta 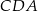 jest równa
jest równa 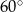 oraz
oraz 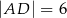 (zobacz rysunek). Oblicz
(zobacz rysunek). Oblicz 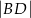 .
.
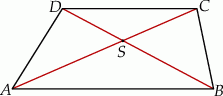
Dany jest trapez 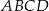 o podstawach
o podstawach 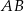 i
i 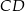 . Przekątne
. Przekątne 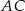 i
i 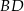 tego trapezu przecinają się w punkcie
tego trapezu przecinają się w punkcie 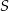 (zobacz rysunek) tak, że
(zobacz rysunek) tak, że 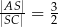 . Pole trójkąta
. Pole trójkąta 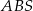 jest równe 12. Oblicz pole trójkąta
jest równe 12. Oblicz pole trójkąta 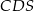 .
.
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego do sześciu oczek. Niech 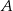 oznacza zdarzenie polegające na tym, że iloczyn liczb oczek wyrzuconych w dwóch rzutach jest równy 12. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że iloczyn liczb oczek wyrzuconych w dwóch rzutach jest równy 12. Oblicz prawdopodobieństwo zdarzenia 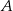 .
.
Dany jest ciąg 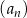 określony wzorem
określony wzorem 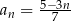 dla każdej liczby naturalnej
dla każdej liczby naturalnej 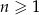 . Trójwyrazowy ciąg
. Trójwyrazowy ciąg 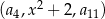 , gdzie
, gdzie  jest liczbą rzeczywistą, jest geometryczny. Oblicz
jest liczbą rzeczywistą, jest geometryczny. Oblicz  oraz iloraz tego ciągu geometrycznego.
oraz iloraz tego ciągu geometrycznego.

