/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 12 marca 2011 Czas pracy: 170 minut
Zadania zamknięte
Liczba 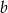 to 95% liczby
to 95% liczby  . Wskaż zdanie fałszywe.
. Wskaż zdanie fałszywe.
A) 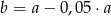 B)
B) 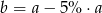 C)
C) 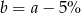 D)
D) 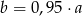
Liczba 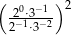 jest równa
jest równa
A) 1 B) 4 C) 9 D) 36
Zbiorem rozwiązań nierówności 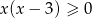 jest
jest
A) 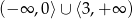
B) 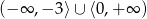
C) 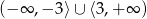
D) 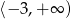
Która z liczb jest największa?
A) 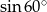 B)
B) 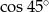 C)
C) 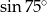 D)
D) 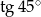
Dane są wielomiany 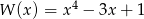 oraz
oraz 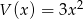 . Wielomian
. Wielomian 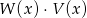 jest równy
jest równy
A) 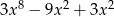 B)
B) 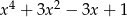 C)
C) 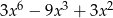 D)
D) 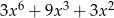
Liczba ![[ ] log lo g (log 5 12) 2 3 2](https://img.zadania.info/zes/0087540/HzesT23x.gif) jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Okrąg o równaniu 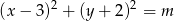 przechodzi przez punkt o współrzędnych
przechodzi przez punkt o współrzędnych 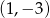 . Wtedy liczba
. Wtedy liczba 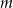 jest równa
jest równa
A) 25 B) 5 C) 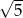 D) 17
D) 17
Zbiorem wartości funkcji 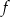 , której wykres przedstawiono poniżej jest
, której wykres przedstawiono poniżej jest
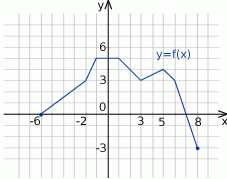
A) 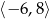 B)
B) 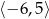 C)
C) 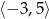 D)
D) 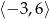
Prosta o równaniu 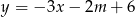 przechodzi przez punkt
przechodzi przez punkt 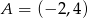 . Wtedy
. Wtedy
A) 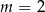 B)
B) 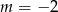 C)
C) 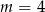 D)
D) 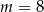
Na rysunku jest przedstawiony wykres funkcji 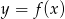 .
.
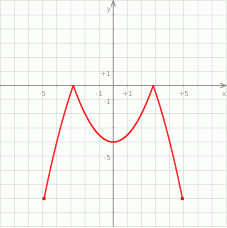
Które równanie ma dokładnie trzy rozwiązania?
A) 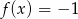 B)
B) 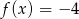 C)
C) 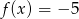 D)
D) 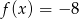
Jaki jest wzór funkcji kwadratowej, której wykres przedstawiono na rysunku?
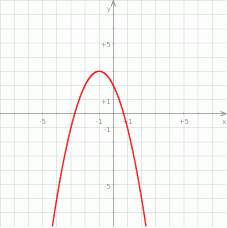
A) 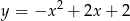 B)
B) 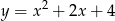 C)
C) 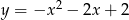 D)
D) 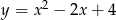
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 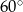 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 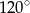 B)
B) 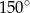 C)
C) 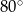 D)
D) 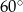
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 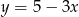 jest równy
jest równy
A) 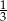 B) -3 C) 5 D)
B) -3 C) 5 D) 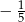
Średnia arytmetyczna pięciu liczb: 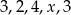 jest równa 3,2. Wtedy
jest równa 3,2. Wtedy
A) 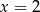 B)
B) 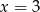 C)
C) 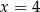 D)
D) 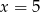
W ciągu arytmetycznym 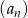 mamy:
mamy: 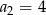 i
i 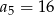 . Oblicz
. Oblicz 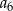 .
.
A) 4 B) 12 C) 22 D) 20
W trójkącie równoramiennym 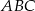 dane są
dane są 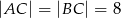 oraz
oraz 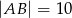 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 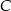 jest równa
jest równa
A) 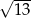 B)
B) 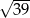 C) 6 D)
C) 6 D) 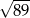
Objętość kuli o promieniu 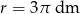 jest równa
jest równa
A) 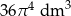 B)
B) 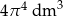 C)
C) 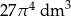 D)
D) 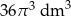
Działka budowlana ma wymiary podane na rysunku.
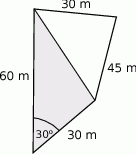
Powierzchnia zacieniowanego trójkąta jest równa
A) 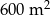 B)
B) 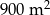 C)
C) 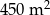 D)
D) 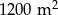
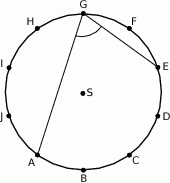
Punkty 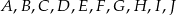 dzielą okrąg o środku
dzielą okrąg o środku 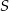 na 10 równych łuków. Oblicz miarę kąta wpisanego
na 10 równych łuków. Oblicz miarę kąta wpisanego 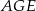 zaznaczonego na rysunku.
zaznaczonego na rysunku.
A) 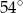 B)
B) 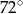 C)
C) 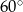 D)
D) 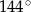
Wszystkich liczb naturalnych dwucyfrowych, które są podzielne przez 7 lub przez 10, jest
A) 24 B) 21 C) 23 D) 22
Zadania otwarte
Rozwiąż nierówność 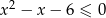 .
.
Rzucamy dwa razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w pierwszym rzucie wypadnie podzielna przez 3 liczba oczek.
Kąt  jest ostry i
jest ostry i 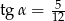 . Oblicz
. Oblicz 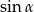 .
.
Wyznacz równanie symetralnej odcinka o końcach 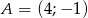 i
i 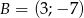 .
.
Oblicz pole sześciokąta foremnego o boku długości 2.
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku.
Wykaż, że liczba 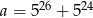 jest podzielna przez 130.
jest podzielna przez 130.
Wyznacz pole trójkąta równobocznego, którego wysokość jest o 2 cm krótsza od boku tego trójkąta.
Wyznacz równanie okręgu wpisanego w kwadrat 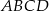 , gdzie
, gdzie 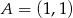 i
i 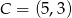 .
.
Trzy liczby tworzą ciąg arytmetyczny. Ich suma jest równa 45. Jeśli pierwszą i trzecią liczbę pozostawimy bez zmian, a drugą pomniejszymy o 3 to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Oblicz wyrazy ciągu arytmetycznego.
W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 12 cm, kąt między wysokościami przeciwległych ścian bocznych ma miarę 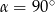 . Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt
. Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt  .
.

