/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki (OKE Poznań)
poziom podstawowy 14 stycznia 2014 Czas pracy: 170 minut
Zadania zamknięte
Dane są liczby 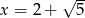 i
i 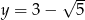 . Iloraz
. Iloraz 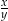 można zapisać w postaci:
można zapisać w postaci:
A) 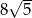 B)
B) 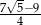 C)
C) 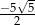 D)
D) 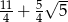
Zbiorem rozwiązań nierówności 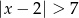 jest:
jest:
A) 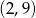 B)
B) 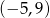 C)
C) 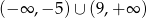 D)
D) 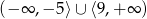
Jeżeli 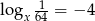 to liczba
to liczba  jest równa
jest równa
A) 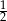 B)
B) 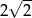 C) 2 D) 4
C) 2 D) 4
Aby otrzymać wielomian 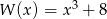 , należy pomnożyć wielomian
, należy pomnożyć wielomian 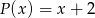 przez wielomian:
przez wielomian:
A) 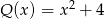 B)
B) 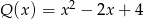 C)
C) 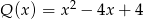 D)
D) 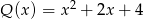
Miejscem zerowym funkcji 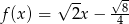 jest liczba:
jest liczba:
A) 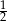 B)
B) 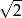 C)
C) 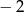 D) 2
D) 2
Najmniejszą liczbą naturalną, która nie spełnia nierówności 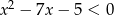 jest
jest
A) 0 B) 3 C) 7 D) 8
Liczba 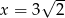 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 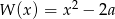 , gdy
, gdy  jest równe
jest równe
A) 18 B) 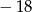 C) 9 D)
C) 9 D) 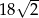
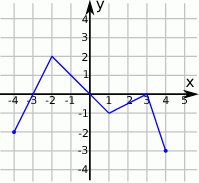
Rysunek przedstawia wykres pewnej funkcji 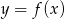 , określonej dla
, określonej dla 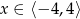 . Zbiór wszystkich argumentów, dla których funkcja
. Zbiór wszystkich argumentów, dla których funkcja 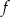 przyjmuje wartości niedodatnie, to zbiór:
przyjmuje wartości niedodatnie, to zbiór:
A) 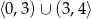
B) 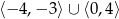
C) 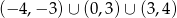
D) 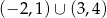
Trzydziesty wyraz ciągu arytmetycznego 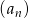 jest równy 4, a trzydziesty piąty wyraz tego ciągu jest równy 7. Wówczas różnica ciągu
jest równy 4, a trzydziesty piąty wyraz tego ciągu jest równy 7. Wówczas różnica ciągu 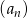 jest równa
jest równa
A) 5 B) 3 C)  D)
D) 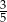
Dany jest ciąg geometryczny 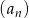 , w którym
, w którym 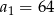 i
i 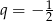 . Wówczas
. Wówczas
A) 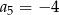 B)
B) 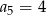 C)
C) 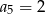 D)
D) 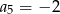
W trójkącie prostokątnym o bokach 6, 8, 10, tangens najmniejszego kąta jest równy:
A) 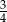 B)
B) 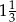 C)
C) 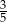 D)
D) 
Miara kąta  , zaznaczonego na rysunku, jest równa
, zaznaczonego na rysunku, jest równa
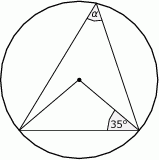
A) 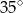 B)
B) 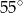 C)
C) 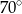 D)
D) 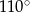
Długość odcinka 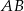 , równoległego do odcinka
, równoległego do odcinka 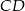 , jest równa:
, jest równa:
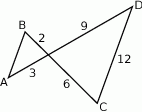
A) 6 B) 3 C) 2 D) 4
Pole koła opisanego na trójkącie równobocznym o wysokości 9 jest równe
A) 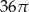 B)
B) 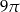 C)
C) 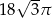 D)
D) 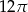
W trapezie prostokątnym kąt ostry ma miarę 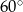 , a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
, a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
A) 6 B) 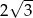 C)
C) 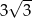 D)
D) 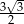
Prostą prostopadłą do prostej 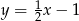 i przechodzącą przez punkt
i przechodzącą przez punkt 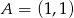 opisuje równanie:
opisuje równanie:
A) 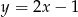 B)
B) 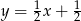 C)
C) 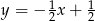 D)
D) 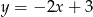
Długość odcinka 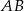 , którego wierzchołki mają współrzędne
, którego wierzchołki mają współrzędne 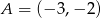 i
i 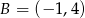 , jest równa:
, jest równa:
A) 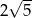 B)
B) 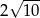 C)
C) 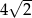 D)
D) 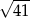
Objętość kuli o promieniu 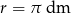 jest równa
jest równa
A) 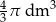 B)
B) 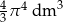 C)
C) 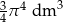 D)
D) 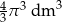
W pudełku są 4 kule białe i  kul czerwonych. Prawdopodobieństwo wylosowania kuli czerwonej jest równe
kul czerwonych. Prawdopodobieństwo wylosowania kuli czerwonej jest równe  , gdy
, gdy
A) 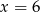 B)
B) 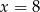 C)
C) 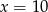 D)
D) 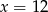
Objętość walca, w którym wysokość jest trzykrotnie dłuższa od promienia podstawy, jest równa 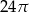 . Zatem promień podstawy tego walca jest ma długość:
. Zatem promień podstawy tego walca jest ma długość:
A) 4 B) 8 C) 2 D) 6
Zadania otwarte
Wyznacz wszystkie liczby naturalne spełniające nierówność: 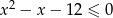 .
.
Liczby 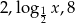 są (w podanej kolejności) wyrazami ciągu arytmetycznego. Wyznacz
są (w podanej kolejności) wyrazami ciągu arytmetycznego. Wyznacz  .
.
Uzasadnij, że 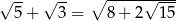 .
.
Wyznacz dziedzinę wyrażenia wymiernego: 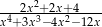 .
.
Na bokach trójkąta prostokątnego zbudowano trójkąty równoboczne. Wykaż, że pole figury zbudowanej na przeciwprostokątnej jest równe sumie pól figur zbudowanych na przyprostokątnych.
Spośród dodatnich liczb dwucyfrowych losujemy kolejno bez zwracania dwie liczby. Oblicz prawdopodobieństwo wylosowania dwóch liczb parzystych.
Okrąg o środku w punkcie 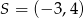 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 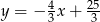 . Oblicz współrzędne punktu styczności.
. Oblicz współrzędne punktu styczności.
Trójkąty prostokątne 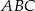 i
i 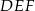 są podobne. Przyprostokątne trójkąta
są podobne. Przyprostokątne trójkąta 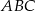 mają długości 5 i 12, a przeciwprostokątna trójkąta
mają długości 5 i 12, a przeciwprostokątna trójkąta 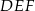 ma długość 26. Wyznacz pole trójkąta
ma długość 26. Wyznacz pole trójkąta 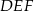 .
.
Pewien kierowca, jadąc z miasta 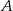 do miasta
do miasta 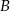 , zmierzył czas i prędkość jazdy. Drogę powrotną pokonał z prędkością o 12 km/h większą, w czasie o 12 minut krótszym. Z jaką średnią prędkością wracał kierowca do miasta
, zmierzył czas i prędkość jazdy. Drogę powrotną pokonał z prędkością o 12 km/h większą, w czasie o 12 minut krótszym. Z jaką średnią prędkością wracał kierowca do miasta 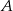 , jeżeli wiadomo, że miasta te są oddalone od siebie o 117 km?
, jeżeli wiadomo, że miasta te są oddalone od siebie o 117 km?
W graniastosłupie prawidłowym czworokątnym 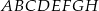 połączono punkty będące środkami krawędzi
połączono punkty będące środkami krawędzi 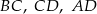 i
i 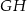 . Wyznacz objętość powstałej bryły wiedząc, że
. Wyznacz objętość powstałej bryły wiedząc, że 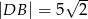 i kąt
i kąt 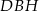 ma miarę
ma miarę 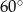 .
.