/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony 6 czerwca 2012 Czas pracy: 180 minut
Rozwiąż nierówność 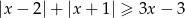 .
.
Wielomian 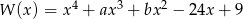 jest kwadratem wielomianu
jest kwadratem wielomianu 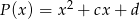 . Oblicz
. Oblicz  oraz
oraz 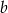 .
.
Kąt  jest taki, że
jest taki, że 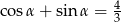 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 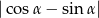 .
.
Wyznacz wszystkie wartości parametru 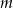 , dla których równanie
, dla których równanie 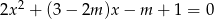 ma dwa różne pierwiastki
ma dwa różne pierwiastki 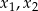 takie, że
takie, że 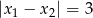 .
.
W ciągu arytmetycznym 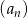 , dla
, dla 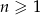 , dane są
, dane są 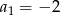 oraz różnica
oraz różnica 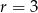 . Oblicz największe
. Oblicz największe  takie, że
takie, że 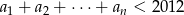 .
.
Udowodnij, że dla dowolnych liczb dodatnich 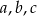 i
i 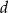 prawdziwa jest nierówność
prawdziwa jest nierówność
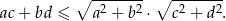
Okrąg jest styczny do osi układu współrzędnych w punktach 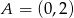 i
i 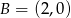 oraz jest styczny do prostej
oraz jest styczny do prostej 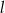 w punkcie
w punkcie 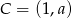 , gdzie
, gdzie 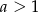 . Wyznacz równanie prostej
. Wyznacz równanie prostej 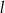 .
.
W czworokącie 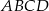 dane są długości boków:
dane są długości boków: 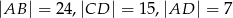 . Ponadto kąty
. Ponadto kąty 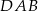 oraz
oraz 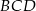 są proste. Oblicz pole tego czworokąta oraz długości jego przekątnych.
są proste. Oblicz pole tego czworokąta oraz długości jego przekątnych.
Oblicz, ile jest liczb naturalnych trzycyfrowych podzielnych przez 6 lub podzielnych przez 15.
Na płaszczyźnie dane są punkty 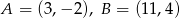 . Na prostej o równaniu
. Na prostej o równaniu 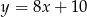 znajdź punkt
znajdź punkt 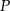 , dla którego suma
, dla którego suma 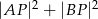 jest najmniejsza.
jest najmniejsza.
Podstawą ostrosłupa 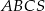 jest trójkąt równoramienny
jest trójkąt równoramienny 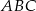 , w którym
, w którym 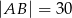 ,
, 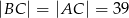 . Spodek wysokości ostrosłupa należy do jego podstawy, a każda wysokość ściany bocznej poprowadzona z wierzchołka
. Spodek wysokości ostrosłupa należy do jego podstawy, a każda wysokość ściany bocznej poprowadzona z wierzchołka 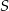 ma długość 26. Oblicz objętość tego ostrosłupa.
ma długość 26. Oblicz objętość tego ostrosłupa.
Zdarzenia losowe 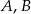 są zawarte w
są zawarte w 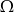 oraz
oraz 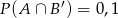 i
i 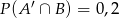 . Wykaż, że
. Wykaż, że 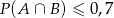 (
(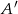 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 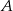 ,
, 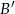 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 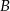 ).
).

