/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 2 kwietnia 2022 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 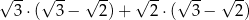 jest równa
jest równa
A) 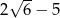 B) 1 C)
B) 1 C) 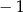 D)
D) 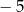
Dana jest funkcja liniowa określona wzorem 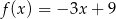 . Wartości ujemne przyjmuje dla:
. Wartości ujemne przyjmuje dla:
A) 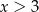 B)
B) 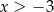 C)
C) 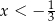 D)
D) 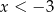
W pojemniku, w którym znajdowały się same monety 1 złotowe zamieniono 38% monet na monety dwuzłotowe oraz pięciozłotowe, przy czym monet dwuzłotowych było dwa razy więcej niż monet pięciozłotowych. W wyniku tej zamiany kwota pieniędzy zgromadzonych w pudełku zwięszyła się o
A) 58% B) 38% C) 76% D) 48%
Liczba 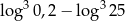 jest równa
jest równa
A) 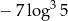 B)
B) 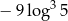 C)
C) 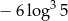 D)
D) 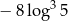
Dana jest funkcja 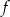 określona wzorem
określona wzorem 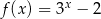 . Wartość funkcji
. Wartość funkcji 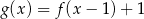 dla argumentu
dla argumentu 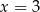 jest równa
jest równa
A) 2 B) 4 C) 6 D) 8
Wskaż, który zbiór przedstawiony na osi liczbowej jest zbiorem liczb spełniających jednocześnie następujące nierówności: 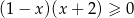 i
i 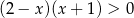 .
.
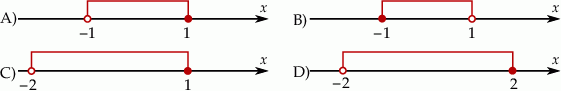
Funkcja liniowa 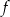 jest określona wzorem
jest określona wzorem 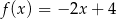 . Wykres funkcji
. Wykres funkcji 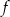 przesunięto wzdłuż osi
przesunięto wzdłuż osi  o 2 jednostki w prawo (tzn. zgodnie ze zwrotem osi), w wyniku czego otrzymano wykres funkcji
o 2 jednostki w prawo (tzn. zgodnie ze zwrotem osi), w wyniku czego otrzymano wykres funkcji 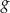 . Funkcja
. Funkcja 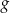 jest określona wzorem
jest określona wzorem
A) 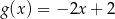 B)
B) 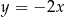 C)
C) 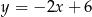 D)
D) 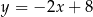
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
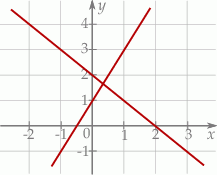
Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.
A) 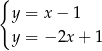 B)
B) 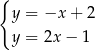 C)
C) 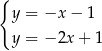 D)
D) 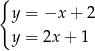
Na rysunku przedstawiono wykres funkcji 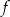 określonej w zbiorze
określonej w zbiorze 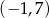 .
.
Wskaż zdanie prawdziwe.
A) Funkcja 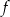 ma trzy miejsca zerowe.
ma trzy miejsca zerowe.
B) Zbiorem wartości funkcji 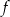 jest
jest 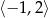 .
.
C) Funkcja 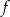 nie przyjmuje wartości 2.
nie przyjmuje wartości 2.
D) Funkcja 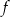 osiąga wartości dodatnie dla argumentów ze zbioru
osiąga wartości dodatnie dla argumentów ze zbioru 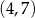 .
.
Po wymnożeniu wyrażeń 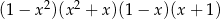 najwyższa potęga
najwyższa potęga  jaką otrzymamy to
jaką otrzymamy to
A) 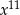 B)
B) 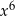 C)
C) 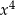 D)
D) 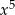
Do kwadratu pewnej liczby rzeczywistej dodano pięciokrotność tej liczby. Która z podanych liczb nie może być wynikiem takiego działania?
A) 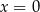 B)
B) 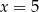 C)
C) 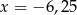 D)
D) 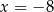
Funkcja 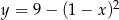 jest rosnąca w przedziale:
jest rosnąca w przedziale:
A) 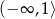 B)
B) 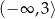 C)
C) 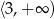 D)
D) 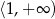
Wartość wyrażenia 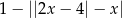 , dla
, dla 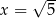 jest równa
jest równa
A) 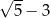 B)
B) 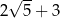 C)
C) 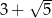 D)
D) 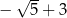
Suma wszystkich liczb całkowitych dodatnich nieparzystych i jednocześnie mniejszych od 1000 jest równa
A) 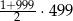 B)
B) 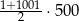 C)
C) 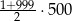 D)
D) 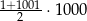
Dany jest nieskończony ciąg geometryczny 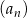 , w którym
, w którym 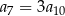 . Wtedy
. Wtedy
A) 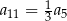 B)
B) 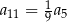 C)
C) 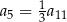 D)
D) 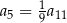
Dla każdego kąta ostrego  iloczyn
iloczyn 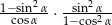 jest równy
jest równy
A) 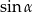 B)
B) 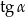 C)
C) 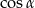 D)
D) 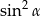
Jednym z pierwiastków równania 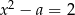 , gdzie
, gdzie  jest liczbą dodatnią, jest liczba
jest liczbą dodatnią, jest liczba 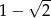 . Zatem drugim pierwiastkiem tego równania jest liczba:
. Zatem drugim pierwiastkiem tego równania jest liczba:
A) 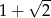 B)
B) 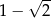 C)
C) 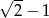 D) 0
D) 0
Jeden z boków równoległoboku ma długość równą 12. Przekątne tego równoległoboku mogą mieć długości
A) 10 i 10 B) 18 i 6 C) 12 i 12 D) 30 i 30
Odcinek 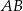 jest średnicą okręgu o środku
jest średnicą okręgu o środku  .
.
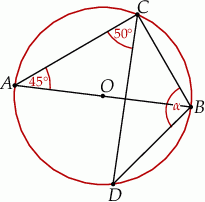
Miara kąta 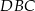 oznaczonego na rysunku literą
oznaczonego na rysunku literą  jest równa
jest równa
A) 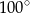 B)
B) 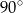 C)
C) 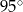 D)
D) 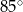
W trapezie prostokątnym podstawy mają długości 9 i 12, a dłuższa przekątna ma długość 13 (zobacz rysunek).
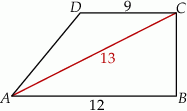
Dłuższe ramię trapezu ma więc długość
A) 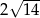 B)
B) 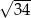 C)
C) 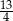 D)
D) 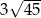
Prosta przechodząca przez punkt 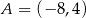 i początek układu współrzędnych jest prostopadła do prostej o równaniu
i początek układu współrzędnych jest prostopadła do prostej o równaniu
A) 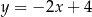 B)
B) 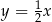 C)
C) 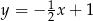 D)
D) 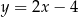
Prosta 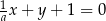 jest równoległa do prostej
jest równoległa do prostej 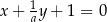 . Wtedy
. Wtedy
A) 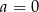 B)
B) 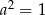 C)
C) 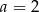 D)
D) 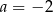
Punkty 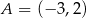 i
i 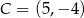 są końcami przekątnej kwadratu
są końcami przekątnej kwadratu 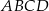 . Promień okręgu opisanego na tym kwadracie jest równy
. Promień okręgu opisanego na tym kwadracie jest równy
A) 100 B) 50 C) 10 D) 5
Pole figury 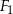 złożonej z dwóch stycznych zewnętrznie kół o promieniach 3 i 5 jest równe polu figury
złożonej z dwóch stycznych zewnętrznie kół o promieniach 3 i 5 jest równe polu figury 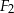 złożonej z dwóch stycznych zewnętrznie kół o promieniach długości
złożonej z dwóch stycznych zewnętrznie kół o promieniach długości  (zobacz rysunek).
(zobacz rysunek).
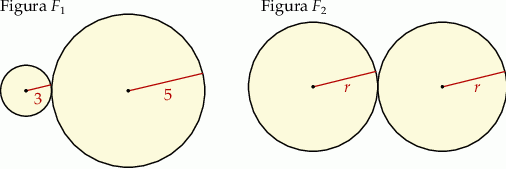
Długość  promienia jest równa
promienia jest równa
A) 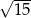 B) 4 C)
B) 4 C) 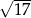 D) 6
D) 6
Graniastosłup prawidłowy ma 42 krawędzie. Długość każdej z tych krawędzi jest równa 4. Pole powierzchni bocznej tego graniastosłupa jest równe
A) 176 B) 192 C) 224 D) 336
Pan Jakub ma 8 marynarek, 5 par różnych spodni i 9 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 240 B) 22 C) 360 D) 90
W pudełku znajdują się tylko kule białe, kule czerwone i kule zielone. Prawdopodobieństwo wylosowania z pudełka kuli zielonej jest dwa razy większe niż prawdopodobieństwo wylosowania kuli czerwonej i dwa razy mniejsze niż wylosowanie kuli białej. Prawdopodobieństwo wylosowania z pudełka kuli zielonej jest równe
A) 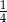 B)
B) 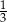 C)
C) 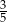 D)
D) 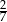
Mediana niemalejącego zestawu danych 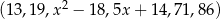 jest równa 40. Zatem
jest równa 40. Zatem
A) istnieją więcej niż dwie możliwe wartości liczby  .
.
B) istnieją dokładnie dwie możliwe wartości liczby  .
.
C) istnieje dokładnie jedna możliwa wartość liczby  .
.
D) nie istnieje liczba  spełniająca podany warunek.
spełniająca podany warunek.
Zadania otwarte
Suma dwóch liczb jest równa 7 i jest o 2 mniejsza od ich iloczynu. Wyznacz te liczby.
Wierzchołkami trójkąta 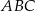 są punkty
są punkty 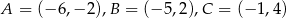 . Oblicz długość środkowej
. Oblicz długość środkowej 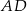 .
.
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 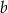 spełniona jest nierówność
spełniona jest nierówność
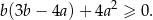
Rozwiąż równanie
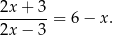
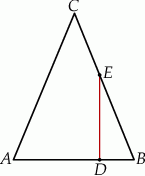
W trójkącie 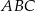 boki
boki 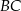 i
i 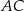 są równej długości. Prosta
są równej długości. Prosta 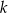 jest prostopadła do podstawy
jest prostopadła do podstawy 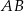 tego trójkąta i przecina boki
tego trójkąta i przecina boki 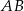 oraz
oraz 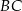 w punktach – odpowiednio –
w punktach – odpowiednio – 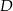 i
i 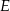 . Oblicz stosunek pola czworokąta
. Oblicz stosunek pola czworokąta 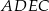 do pola trójkąta
do pola trójkąta 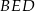 jeżeli
jeżeli 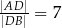 .
.
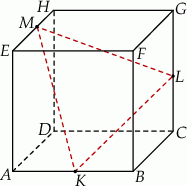
Punkty 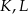 i
i 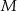 są środkami krawędzi
są środkami krawędzi 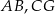 i
i 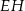 sześcianu
sześcianu  o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta
o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta  .
.
Trzy liczby dodatnie tworzą rosnący ciąg geometryczny o sumie równej 62. Suma logarytmów dziesiętnych tych liczb jest równa 3. Wyznacz te liczby.

