/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 10 marca 2012 Czas pracy: 180 minut
Rozwiąż nierówność 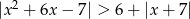 .
.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 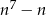 jest podzielna przez 7.
jest podzielna przez 7.
Dla jakich wartości parametru 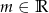 wierzchołek paraboli
wierzchołek paraboli 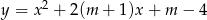 leży najbliżej prostej
leży najbliżej prostej 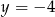 ?
?
W trójkącie 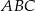 środkowa
środkowa 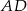 jest prostopadła do boku
jest prostopadła do boku 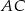 . Kąt
. Kąt 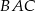 ma miarę
ma miarę 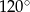 . Wykaż, że
. Wykaż, że 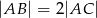 .
.
Rozwiąż równanie 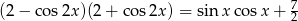 w przedziale
w przedziale 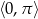 .
.
Różnica ciągu arytmetycznego 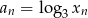 jest równa
jest równa 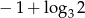 . Oblicz
. Oblicz 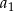 jeżeli wiadomo, że
jeżeli wiadomo, że
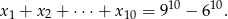
Wielomiany 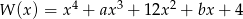 oraz
oraz 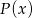 są wielomianami o współczynnikach całkowitych, przy czym
są wielomianami o współczynnikach całkowitych, przy czym ![W (x ) = [P (x)]2](https://img.zadania.info/zes/0087772/HzesT20x.gif) . Wyznacz wszystkie możliwe wartości
. Wyznacz wszystkie możliwe wartości  i
i 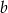 .
.
Udowodnij, że średnica okręgu wpisanego w trapez równoramienny, ma długość równą średniej geometrycznej długości podstaw trapezu.
Z punktu 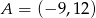 poprowadzono styczne do okręgu o równaniu
poprowadzono styczne do okręgu o równaniu 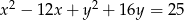 . Oblicz długość odcinka łączącego punkty styczności.
. Oblicz długość odcinka łączącego punkty styczności.
Krawędź boczna ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta między sąsiednimi ścianami bocznymi.
Ze zbioru 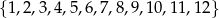 losujemy podzbiór trójelementowy. Jakie jest prawdopodobieństwo, że iloczyn liczb będących elementami wylosowanego podzbioru jest liczbą parzystą?
losujemy podzbiór trójelementowy. Jakie jest prawdopodobieństwo, że iloczyn liczb będących elementami wylosowanego podzbioru jest liczbą parzystą?

