/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 23 kwietnia 2022 Czas pracy: 170 minut
Zadania zamknięte
Liczba 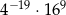 jest równa
jest równa
A) 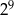 B)
B) 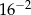 C)
C) 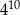 D)
D) 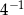
Liczba 609 stanowi 140% liczby  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 420 B) 435 C) 468 D) 406
Wiadomo, że 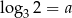 oraz
oraz 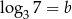 . Zatem
. Zatem 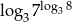 jest równy
jest równy
A) 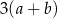 B)
B) 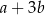 C)
C) 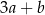 D)
D) 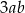
Dla każdej liczby rzeczywistej  wyrażenie
wyrażenie 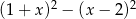 jest równe
jest równe
A) 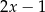 B)
B) 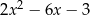 C)
C) 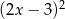 D)
D) 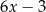
Liczba 3 jest rozwiązaniem równania
A) 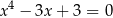 B)
B) 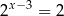 C)
C) 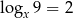 D)
D) 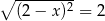
Zbiorem wszystkich rozwiązań nierówności 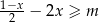 jest przedział
jest przedział 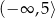 . Liczba
. Liczba 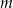 jest więc równa
jest więc równa
A) 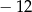 B) 13 C)
B) 13 C) 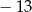 D) 17
D) 17
Rozwiązaniem równania 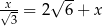 jest liczba
jest liczba
A) 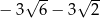 B)
B) 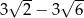 C)
C) 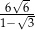 D)
D) 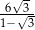
Punkty 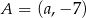 i
i 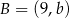 są końcami średnicy okręgu o środku
są końcami średnicy okręgu o środku 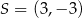 . Wtedy
. Wtedy
A) 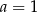 B)
B) 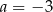 C)
C) 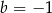 D)
D) 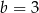
Prosta 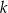 przechodzi przez punkt
przechodzi przez punkt 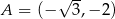 i jest nachylona do osi
i jest nachylona do osi 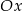 pod kątem
pod kątem 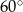 (zobacz rysunek).
(zobacz rysunek).
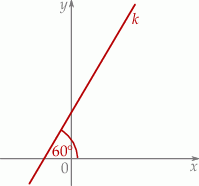
Prosta 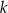 ma równanie
ma równanie
A) 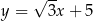 B)
B) 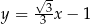 C)
C) 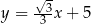 D)
D) 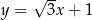
Funkcja 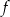 jest określona wzorem
jest określona wzorem 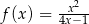 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 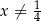 . Wtedy dla argumentu
. Wtedy dla argumentu 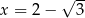 wartość funkcji
wartość funkcji 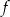 jest równa
jest równa
A) 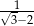 B)
B) 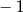 C) 1 D)
C) 1 D) 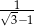
Ciąg geometryczny 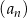 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 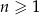 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 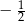 . Wtedy
. Wtedy
A) 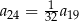 B)
B) 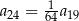 C)
C) 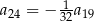 D)
D) 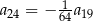
Ciąg 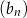 jest określony wzorem
jest określony wzorem 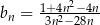 dla każdej liczby naturalnej
dla każdej liczby naturalnej 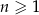 . Liczba niedodatnich wyrazów ciągu
. Liczba niedodatnich wyrazów ciągu 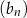 jest równa
jest równa
A) 8 B) 9 C) 13 D) 14
Informacja do zadań 13 i 14
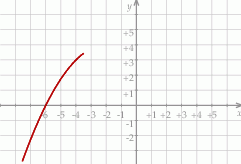
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 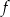 . Jednym z miejsc zerowych tej funkcji jest liczba
. Jednym z miejsc zerowych tej funkcji jest liczba 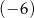 . Do wykresu funkcji
. Do wykresu funkcji 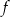 należy punkt
należy punkt 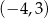 . Prosta o równaniu
. Prosta o równaniu 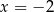 jest osią symetrii paraboli, będącej wykresem funkcji
jest osią symetrii paraboli, będącej wykresem funkcji 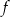 .
.
Drugim miejscem zerowym funkcji 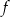 jest liczba
jest liczba
A) 2 B) 1 C) 0 D) 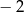
Wartość funkcji 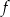 dla argumentu 0 jest równa
dla argumentu 0 jest równa
A) 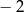 B) 0 C) 3 D) 4
B) 0 C) 3 D) 4
Ciągi 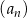 ,
, 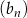 oraz
oraz 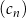 są określone dla każdej liczby naturalnej
są określone dla każdej liczby naturalnej 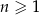 następująco:
następująco:
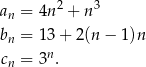
Wskaż zdanie prawdziwe.
A) Ciąg 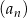 jest arytmetyczny.
jest arytmetyczny.
B) Ciąg 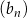 jest arytmetyczny.
jest arytmetyczny.
C) Ciąg 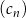 jest arytmetyczny.
jest arytmetyczny.
D) Wśród ciągów 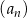 ,
, 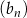 ,
, 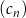 nie ma ciągu arytmetycznego.
nie ma ciągu arytmetycznego.
Para liczb 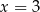 ,
, 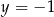 spełnia układ równań
spełnia układ równań
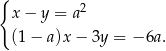
Wtedy  jest równe
jest równe
A) 2 B) 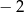 C)
C) 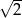 D)
D) 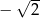
Czworokąt 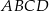 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 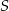 . Bok
. Bok 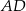 jest średnicą tego okręgu, a miara kąta
jest średnicą tego okręgu, a miara kąta 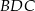 jest równa
jest równa 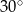 (zobacz rysunek).
(zobacz rysunek).
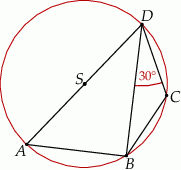
Wtedy miara kąta 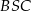 jest równa
jest równa
A) 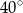 B)
B) 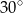 C)
C) 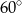 D)
D) 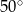
Kąt  jest kątem ostrym i
jest kątem ostrym i 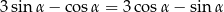 . Zatem
. Zatem
A) 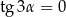 B)
B) 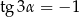 C)
C) 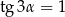 D)
D) 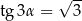
Funkcja liniowa 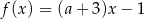 osiąga wartość największą równą
osiąga wartość największą równą 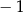 . Wtedy
. Wtedy
A) 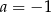 B)
B) 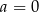 C)
C) 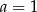 D)
D) 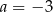
W pewnym trójkącie równoramiennym największy kąt ma miarę 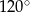 , a ramię ma długość 6 (zobacz rysunek).
, a ramię ma długość 6 (zobacz rysunek).

Najkrótsza wysokość tego trójkąta ma długość równą
A) 4 B) 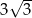 C)
C) 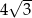 D) 3
D) 3
W układzie współrzędnych dane są dwa punkty 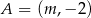 oraz
oraz 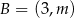 . Współczynnik kierunkowy prostej
. Współczynnik kierunkowy prostej 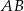 jest równy
jest równy  . Zatem
. Zatem
A) 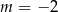 B)
B) 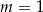 C)
C) 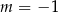 D)
D) 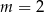
Przekątna 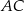 trapezu równoramiennego
trapezu równoramiennego 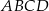 jest prostopadła do ramienia
jest prostopadła do ramienia 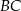 oraz tworzy z ramieniem
oraz tworzy z ramieniem 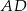 kąt ostry
kąt ostry  . Wysokość trapezu opuszczona z wierzchołka
. Wysokość trapezu opuszczona z wierzchołka 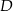 i ramię
i ramię 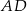 przecinają się pod kątem ostrym
przecinają się pod kątem ostrym 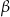 o mierze
o mierze 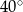 (zobacz rysunek).
(zobacz rysunek).
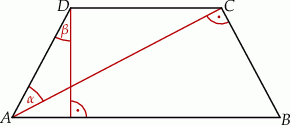
Wtedy kąt  ma miarę
ma miarę
A) 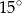 B)
B) 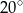 C)
C) 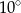 D)
D) 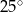
Punkty o współrzędnych: 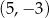 ,
, 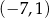 ,
, 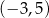 i
i 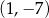 są wierzchołkami prostokąta. Pole tego prostokąta jest równe
są wierzchołkami prostokąta. Pole tego prostokąta jest równe
A) 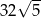 B) 32 C) 64 D)
B) 32 C) 64 D) 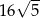
Każdą krawędź czworościanu foremnego wydłużamy dwukrotnie. Pole powierzchni czworościanu zwiększy się
A) dwukrotnie B) czterokrotnie C) ośmiokrotnie D) szesnastokrotnie
Wszystkich liczb naturalnych sześciocyfrowych nieparzystych jest
A) 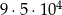 B)
B) 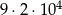 C)
C) 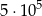 D)
D) 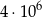
Z wierzchołków sześcianu 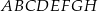 losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te są końcami przekątnej jednej ze ścian sześcianu
losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te są końcami przekątnej jednej ze ścian sześcianu 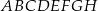 , jest równe
, jest równe
A)  B)
B)  C)
C) 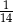 D)
D) 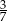
Przekątna sześcianu ma długość 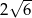 . Objętość tego sześcianu wynosi
. Objętość tego sześcianu wynosi
A) 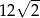 B)
B) 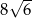 C)
C) 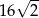 D) 48
D) 48
Średnia arytmetyczna czterech liczb dodatnich: 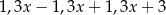 jest równa
jest równa 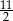 . Wynika stąd, że
. Wynika stąd, że
A) 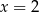 B)
B) 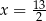 C)
C) 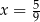 D)
D) 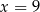
Zadania otwarte
Wyznacz wszystkie liczby całkowite spełniające nierówność 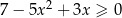 .
.
Wykaż, że dla każdych czterech liczb dodatnich 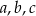 i
i 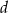 takich, że
takich, że 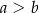 i
i 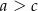 spełniona jest nierówność
spełniona jest nierówność
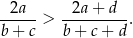
Punkty 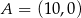 i
i 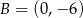 są końcami odcinka
są końcami odcinka 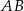 . Prosta
. Prosta 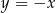 przecina odcinek
przecina odcinek 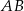 w punkcie
w punkcie 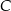 . Oblicz stosunek
. Oblicz stosunek 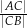 .
.
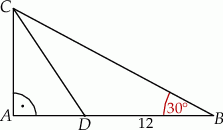
W trójkącie 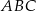 kąt przy wierzchołku
kąt przy wierzchołku 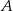 jest prosty, a kąt przy wierzchołku
jest prosty, a kąt przy wierzchołku 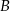 ma miarę
ma miarę 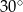 . Na boku
. Na boku 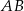 tego trójkąta obrano punkt
tego trójkąta obrano punkt 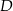 tak, że odcinek
tak, że odcinek 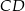 jest dwusieczną kąta przy wierzchołku
jest dwusieczną kąta przy wierzchołku 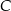 oraz
oraz 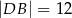 (zobacz rysunek). Oblicz
(zobacz rysunek). Oblicz 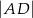 .
.
Dany jest trapez o podstawach długości  oraz
oraz 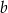 i wysokości
i wysokości 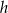 . Każdą z podstaw tego trapezu skrócono o 20%, a wysokość wydłużono tak, że powstał nowy trapez o takim samym polu. Oblicz, o ile procent wydłużono wysokość
. Każdą z podstaw tego trapezu skrócono o 20%, a wysokość wydłużono tak, że powstał nowy trapez o takim samym polu. Oblicz, o ile procent wydłużono wysokość 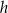 trapezu.
trapezu.
Gracz rzuca dwukrotnie symetryczną sześcienną kostką do gry i oblicza wartość bezwzględną różnicy liczb wyrzuconych oczek. Oblicz prawdopodobieństwo zdarzenia 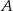 polegającego na tym, że obliczona wartość bezwzględna różnicy wyrzuconych oczek jest równa 3, 4 lub 5.
polegającego na tym, że obliczona wartość bezwzględna różnicy wyrzuconych oczek jest równa 3, 4 lub 5.
Rosnący ciąg arytmetyczny 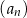 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 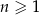 . Suma pierwszych dwunastu wyrazów tego ciągu jest równa 240. Wyrazy
. Suma pierwszych dwunastu wyrazów tego ciągu jest równa 240. Wyrazy 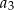 ,
, 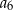 ,
, 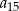 tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na
tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na  –ty wyraz ciągu arytmetycznego
–ty wyraz ciągu arytmetycznego 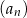 .
.

