/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 3 maja 2014 Czas pracy: 170 minut
Zadania zamknięte
Wskaż nierówność, która opisuje sumę przedziałów zaznaczonych na osi liczbowej.
![]()
A) 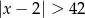 B)
B) 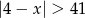 C)
C) 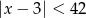 D)
D) 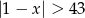
Jeżeli liczba 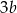 jest o 20% większa od połowy liczby
jest o 20% większa od połowy liczby 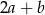 , to liczba
, to liczba  jest większa od
jest większa od 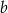 o
o
A) 100% B) 50% C) 80% D) 200%
Liczba 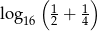 jest równa
jest równa
A) 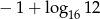 B)
B) 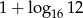 C) 6 D) -6
C) 6 D) -6
Układ równań 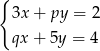 z niewiadomymi
z niewiadomymi  i
i 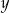 ma nieskończenie wiele rozwiązań. Zatem liczba
ma nieskończenie wiele rozwiązań. Zatem liczba 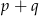 jest równa
jest równa
A) 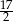 B) 15 C)
B) 15 C) 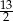 D) 6
D) 6
Która z podanych prostych nie ma punktów wspólnych z trzecią ćwiartką układu współrzędnych?
A) 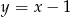 B)
B) 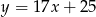 C)
C) 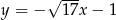 D)
D) 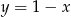
Wykres funkcji kwadratowej 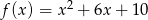 powstaje z wykresu funkcji
powstaje z wykresu funkcji 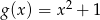 przez przesunięcie o 3 jednostki
przez przesunięcie o 3 jednostki
A) w górę B) w prawo C) w lewo D) w dół
Wyrażenie 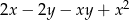 jest równe wyrażeniu
jest równe wyrażeniu
A) 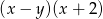 B)
B) 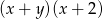 C)
C)  D)
D) 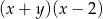
Wykresy funkcji 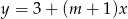 i
i 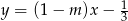 są prostopadłe. Zatem
są prostopadłe. Zatem 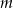
A) jest liczbą ujemną
B) jest liczbą wymierną
C) jest liczbą naturalną
D) jest liczbą niewymierną
Nierówność 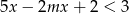 jest spełniona przez każdą liczbę rzeczywistą jeżeli
jest spełniona przez każdą liczbę rzeczywistą jeżeli
A) 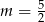 B)
B) 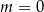 C)
C) 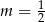 D)
D) 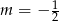
Równania 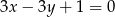 i
i 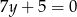 opisują proste w układzie współrzędnych, które
opisują proste w układzie współrzędnych, które
A) są prostopadłe
B) są równoległe
C) przecinają się pod kątem 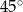
D) przecinają się pod kątem 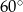
Na rysunku 1 jest przedstawiony wykres funkcji 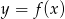 .
.
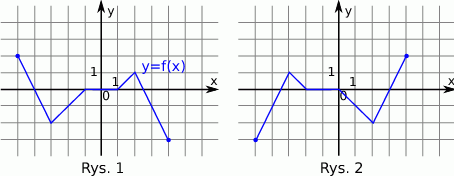
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 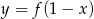 B)
B) 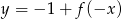 C)
C) 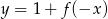 D)
D) 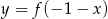
Ciąg 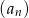 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 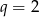 , w którym
, w którym 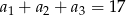 . Suma
. Suma 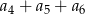 jest równa
jest równa
A) 68 B) 289 C) 34 D) 136
Na tablicy wypisano kolejne wyrazy pewnego ciągu arytmetycznego
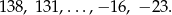
Ile liczb napisano na tablicy?
A) 21 B) 24 C) 23 D) 22
Wartość wyrażenia 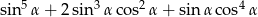 jest równa
jest równa
A) 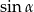 B)
B) 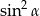 C)
C) 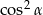 D)
D) 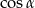
Bok 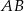 czworokąta
czworokąta 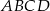 wpisanego w okrąg jest średnicą okręgu oraz
wpisanego w okrąg jest średnicą okręgu oraz 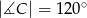 .
.
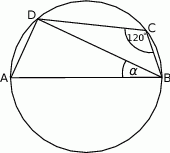
Zatem kąt  ma miarę
ma miarę
A) 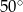 B)
B) 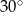 C)
C) 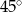 D)
D) 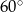
Równanie 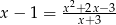
A) ma rozwiązania ujemne
B) jest sprzeczne
C) ma mniej niż 5 rozwiązań
D) spełnia każda liczba rzeczywista
Punkty 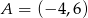 i
i 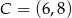 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 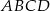 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 104 B) 4 C) 52 D) 26
Dwa przeciwległe wierzchołki prostokąta mają współrzędne 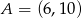 i
i 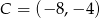 . Środek okręgu opisanego na tym prostokącie leży na prostej
. Środek okręgu opisanego na tym prostokącie leży na prostej
A) 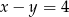 B)
B) 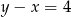 C)
C) 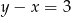 D)
D) 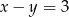
Do okręgu o środku 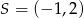 i promieniu
i promieniu 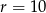 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 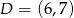 B)
B) 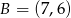 C)
C) 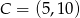 D)
D) 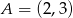
Która z podanych liczb nie może być liczbą krawędzi graniastosłupa?
A) 13629 B) 17023 C) 37035 D) 26919
Objętość kuli stycznej do wszystkich ścian sześcianu o krawędzi długości 6 jest równa
A) 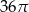 B)
B) 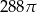 C)
C) 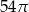 D)
D) 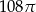
Losujemy jedną liczbę trzycyfrową. Prawdopodobieństwo 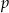 otrzymania liczby, której cyfry to 1,2,3 (w dowolnej kolejności) spełnia warunek
otrzymania liczby, której cyfry to 1,2,3 (w dowolnej kolejności) spełnia warunek
A) 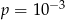 B)
B) 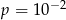 C)
C) 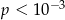 D)
D) 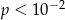
Liczba 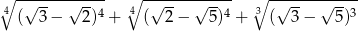 jest równa
jest równa
A) 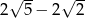 B)
B) 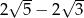 C)
C) 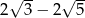 D)
D) 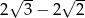
Mediana danych zawartych w tabeli liczebności jest równa 3.
| Wartość | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczebność | 3 | 4 |  | 1 | 2 | 6 |
Zatem  może być równe
może być równe
A) 3 B) 1 C) 2 D) 0
Prostopadłościan dzielimy na części prowadząc dwie płaszczyzny równoległe do jego podstaw, które dzielą krawędź boczną w stosunku 5:1:2. Jaki procent objętości całego prostopadłościanu stanowi objętość najmniejszej z utworzonych części?
A) 12,5% B) 17% C) 15% D) 25%
Zadania otwarte
Wyznacz punkty wspólne okręgu 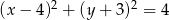 oraz prostej
oraz prostej 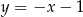 .
.
Posługując się wzorem 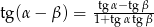 oblicz
oblicz 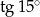 .
.
Udowodnij, że jeżeli 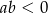 to
to 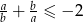 .
.
Wiadomo, że funkcja liniowa 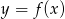 przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy
przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy 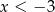 . Ponadto,
. Ponadto, 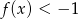 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 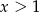 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 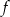 .
.
Rozwiąż nierówność 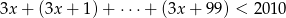 , gdzie lewa strona jest sumą kolejnych wyrazów ciągu arytmetycznego.
, gdzie lewa strona jest sumą kolejnych wyrazów ciągu arytmetycznego.
Na bokach trójkąta równobocznego zbudowano dwa kwadraty w sposób pokazany na rysunku.
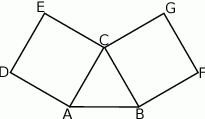
Wykaż, że punkty 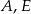 i
i 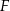 są wierzchołkami trójkąta prostokątnego.
są wierzchołkami trójkąta prostokątnego.
W prostokącie 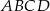 , w którym
, w którym 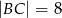 połączono wierzchołek
połączono wierzchołek 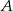 z punktem
z punktem 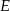 leżącym na boku
leżącym na boku 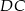 . Odcinek ten przeciął przekątną
. Odcinek ten przeciął przekątną 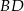 w punkcie
w punkcie 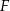 .
.
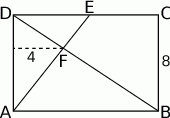
Wiedząc, że odległość punktu 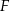 od boku
od boku 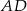 jest równa 4, oraz że
jest równa 4, oraz że 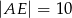 oblicz długość boku
oblicz długość boku 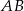 prostokąta.
prostokąta.
Na prostej 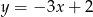 wyznacz punkt, którego suma kwadratów odległości od osi układu współrzędnych jest najmniejsza.
wyznacz punkt, którego suma kwadratów odległości od osi układu współrzędnych jest najmniejsza.
Oblicz objętość graniastosłupa prawidłowego trójkątnego, w którym krawędź podstawy ma długość 1, a przekątna ściany bocznej tworzy z sąsiednią ścianą kąt o mierze 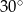 .
.

