/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 3 marca 2012 Czas pracy: 170 minut
Zadania zamknięte
Pierwsza rata, która stanowi 11% ceny telewizora, jest równa 341 zł. Telewizor kosztuje
A) 2759 zł B) 2910 zł C) 3100 zł D) 3159 zł
Rozwiązaniem równania 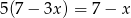 jest:
jest:
A) 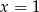 B)
B) 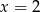 C)
C) 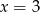 D)
D) 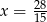
Wyrażenie 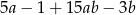 jest równe iloczynowi
jest równe iloczynowi
A) 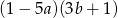 B)
B) 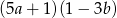 C)
C) 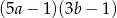 D)
D) 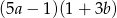
Jedno rozwiązanie ma równanie
A) 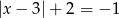 B)
B) 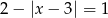 C)
C) 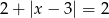 D)
D) 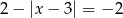
Wyrażenie 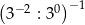 jest równe
jest równe
A) 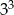 B)
B) 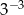 C)
C) 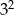 D)
D) 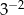
Układ równań 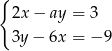 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 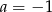 B)
B) 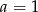 C)
C) 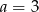 D)
D) 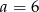
Wskaż, który zbiór przedstawiony na osi liczbowej jest zbiorem liczb spełniających jednocześnie następujące nierówności: 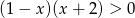 i
i 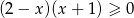 .
.
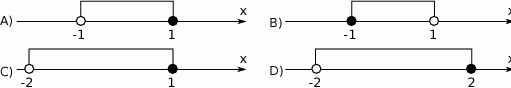
Funkcja 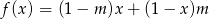 jest rosnąca, gdy
jest rosnąca, gdy
A) 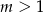 B)
B) 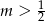 C)
C) 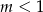 D)
D) 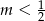
Liczba 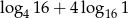 jest równa
jest równa
A) 16 B) 2 C) 4 D) 6
Wykresem funkcji kwadratowej 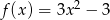 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie
A) 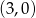 B)
B) 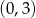 C)
C) 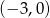 D)
D) 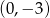
Do wykresu funkcji 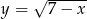 należy punkt
należy punkt 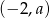 . Wówczas
. Wówczas
A) 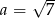 B)
B) 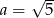 C)
C) 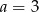 D)
D) 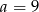
Miary kątów czworokąta tworzą ciąg arytmetyczny o pierwszym wyrazie 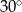 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 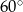 B)
B) 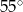 C)
C) 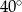 D)
D) 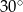
Ile jest liczb naturalnych czterocyfrowych, których kolejne cyfry tworzą ciąg arytmetyczny o różnicy 2 lub 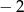 ?
?
A) 7 B) 6 C) 12 D) 9
Liczby 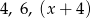 są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas liczba
są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas liczba  jest równa:
jest równa:
A) 9 B) 10 C) 13 D) 5
Przekątne rombu mają długości 12 i 10. Obwód tego rombu jest równy
A) 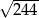 B)
B) 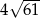 C)
C) 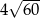 D)
D) 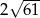
Jaką miarę ma kąt  ?
?
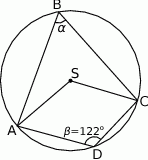
A) 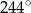 B)
B) 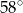 C)
C) 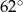 D)
D) 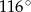
Krawędź sześcianu ma długość 6. Długość przekątnej tego sześcianu jest równa:
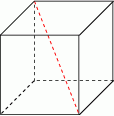
A) 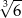 B)
B) 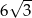 C)
C) 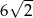 D)
D) 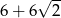
Prosta 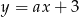 jest równoległa do prostej
jest równoległa do prostej 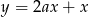 . Wtedy
. Wtedy
A) 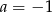 B)
B) 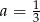 C)
C) 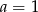 D)
D) 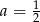
Liczba przekątnych o długości 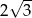 w sześciokącie foremnym o boku długości 2 jest równa
w sześciokącie foremnym o boku długości 2 jest równa
A) 0 B) 3 C) 6 D) 9
Nie istnieje kąt ostry  , taki, że
, taki, że
A) 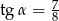 B)
B) 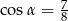 C)
C) 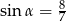 D)
D) 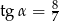
Promień okręgu wpisanego w trójkąt równoboczny jest o 2 krótszy od promienia okręgu opisanego na tym trójkącie. Wysokość trójkąta ma więc długość
A) 6 B) 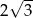 C)
C) 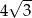 D) 12
D) 12
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Pole powierzchni całkowitej tego graniastosłupa jest równe 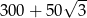 . Długość krawędzi tego graniastosłupa jest równa
. Długość krawędzi tego graniastosłupa jest równa
A) 12 B) 10 C) 9 D) 6
Które z poniższych zdań nie jest prawdziwe?
A) W każdy romb można wpisać okrąg.
B) W każdy prostokąt można wpisać okrąg.
C) Na każdym prostokącie można opisać okrąg.
D) W każdy deltoid można wpisać okrąg.
Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo wyrzucenia w obu rzutach liczby oczek podzielnej przez 3 jest równe
A) 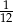 B)
B) 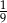 C)
C) 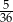 D)
D) 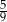
Medianą danych 1,2,3,5,7,7,8,9 jest liczba
A) 4 B) 5 C) 6 D) 7
Zadania otwarte
Rozwiąż równanie 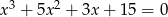 .
.
Wykaż, że jeżeli 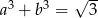 i
i 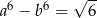 to
to 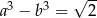 .
.
Kąt  jest kątem ostrym i
jest kątem ostrym i 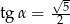 . Oblicz
. Oblicz 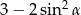 .
.
Wyznacz równanie prostej zawierającej środkową 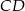 trójkąta
trójkąta 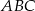 , którego wierzchołkami są punkty:
, którego wierzchołkami są punkty: 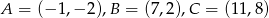 .
.
W równoległoboku 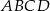 , w którym
, w którym 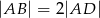 punkt
punkt 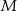 jest środkiem boku
jest środkiem boku 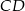 . Wykaż, że trójkąt
. Wykaż, że trójkąt 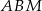 jest prostokątny.
jest prostokątny.
Ze zbioru 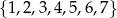 losujemy dwa razy po jednej liczbie bez zwracania. Z wylosowanych liczb tworzymy liczbę dwucyfrową w następujący sposób: mniejsza z wylosowanych liczb jest cyfrą jedności, a większa cyfrą dziesiątek utworzonej liczby. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 7.
losujemy dwa razy po jednej liczbie bez zwracania. Z wylosowanych liczb tworzymy liczbę dwucyfrową w następujący sposób: mniejsza z wylosowanych liczb jest cyfrą jedności, a większa cyfrą dziesiątek utworzonej liczby. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 7.
Współczynniki 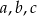 funkcji kwadratowej
funkcji kwadratowej 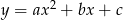 w podanej kolejności tworzą ciąg arytmetyczny. Jednym z miejsc zerowych tej funkcji jest
w podanej kolejności tworzą ciąg arytmetyczny. Jednym z miejsc zerowych tej funkcji jest 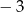 . Punkt o współrzędnych
. Punkt o współrzędnych 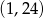 należy do wykresu funkcji. Znajdź drugie miejsce zerowe oraz wartości współczynników
należy do wykresu funkcji. Znajdź drugie miejsce zerowe oraz wartości współczynników 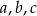 .
.
Dwa samochody osobowe wyjechały z miast 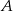 i
i 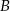 oddalonych od siebie o 480 km. Samochód jadący z miasta
oddalonych od siebie o 480 km. Samochód jadący z miasta 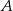 do miasta
do miasta 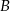 wyjechał o pół godziny wcześniej niż samochód jadący z miasta
wyjechał o pół godziny wcześniej niż samochód jadący z miasta 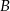 do miasta
do miasta 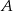 i jechał z prędkością o 16 km/h mniejszą. Samochody te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te samochody.
i jechał z prędkością o 16 km/h mniejszą. Samochody te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te samochody.

