/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy
(technikum) 21 marca 2015 Czas pracy: 170 minut
Zadania zamknięte
Liczba 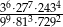 jest równa
jest równa
A) 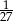 B) 243 C) 27 D)
B) 243 C) 27 D) 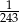
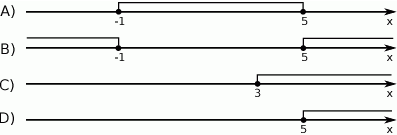
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 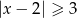 .
.
W solance, która zawierała 8% soli zwiększono zawartość soli o 187,5%. Stężenie soli w otrzymanym roztworze wynosi
A) 23% B) 20% C) 18% D) 25%
Rozwiązaniem równania 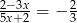 jest
jest
A) 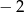 B)
B) 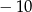 C)
C) 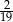 D)
D) 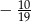
Prosta o równaniu 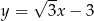 jest nachylona do osi
jest nachylona do osi 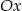 pod kątem
pod kątem
A) 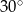 B)
B) 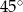 C)
C) 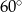 D)
D) 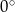
Wykres funkcji kwadratowej 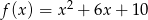 powstaje z wykresu funkcji
powstaje z wykresu funkcji 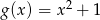 przez przesunięcie o 3 jednostki
przez przesunięcie o 3 jednostki
A) w prawo B) w lewo C) w górę D) w dół
Dla pewnych liczb  i
i 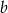 zachodzą równości:
zachodzą równości: 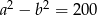 i
i 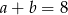 . Dla tych liczb
. Dla tych liczb  i
i 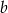 wartość wyrażenia
wartość wyrażenia 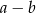 jest równa
jest równa
A) 25 B) 16 C) 10 D) 2
Zbiorem wartości funkcji kwadratowej 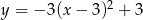 jest
jest
A) 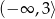 B)
B) 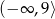 C)
C) 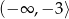 D)
D) 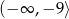
Wykres funkcji 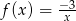 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) II i IV B) II i III C) I i III D) I i II
Proste o równaniach 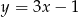 oraz
oraz 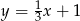
A) pokrywają się
B) przecinają się pod kątem innym niż prosty
C) są prostopadłe
D) są równoległe i różne
Dane są wielomiany 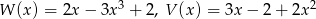 . Stopień wielomianu
. Stopień wielomianu 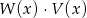 jest równy
jest równy
A) 6 B) 4 C) 5 D) 3
Kąt  jest ostry i
jest ostry i 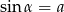 . Liczba
. Liczba  może być równa
może być równa
A) 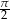 B)
B) 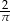 C)
C) 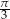 D)
D) 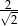
W ciągu arytmetycznym 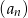 dane są:
dane są: 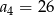 i
i 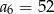 . Wtedy wyraz
. Wtedy wyraz 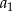 jest równy
jest równy
A) 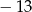 B) 0 C) 13 D)
B) 0 C) 13 D) 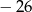
Suma miar kąta wpisanego i kąta środkowego, opartych na 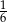 okręgu, jest równa
okręgu, jest równa
A) 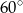 B)
B) 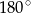 C)
C) 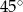 D)
D) 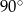
Liczba 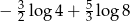 jest równa
jest równa
A) 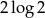 B)
B) 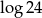 C) 2 D)
C) 2 D) 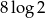
Punkty 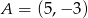 ,
, 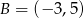 ,
, 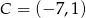 i
i 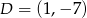 są wierzchołkami prostokąta
są wierzchołkami prostokąta 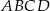 . Pole tego prostokąta jest równe
. Pole tego prostokąta jest równe
A) 16 B) 32 C) 64 D) 96
Średnice 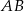 i
i 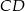 okręgu o środku
okręgu o środku 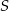 przecinają się pod kątem
przecinają się pod kątem 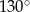 (tak jak na rysunku).
(tak jak na rysunku).
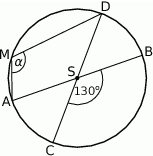
Miara kąta  jest równa
jest równa
A) 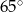 B)
B) 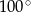 C)
C) 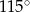 D)
D) 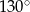
Ogród ma kształt prostokąta o bokach długości 20 m i 40 m. Na dwóch końcach przekątnej tego prostokąta wbito słupki. Odległość między tymi słupkami jest
A) równa 40 m
B) większa niż 50 m
C) większa niż 40 m i mniejsza niż 45 m
D) większa niż 45 m i mniejsza niż 50 m
Punkt 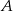 ma współrzędne
ma współrzędne 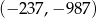 . Punkt
. Punkt 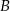 jest symetryczny do punktu
jest symetryczny do punktu 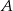 względem początku układu współrzędnych, a punkt
względem początku układu współrzędnych, a punkt 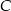 jest symetryczny do punktu
jest symetryczny do punktu 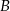 względem osi
względem osi 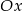 . Punkt
. Punkt 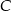 ma współrzędne
ma współrzędne
A) 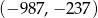 B)
B) 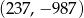 C)
C) 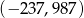 D)
D) 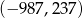
Grupa przypadkowych przechodniów została poproszona o odpowiedź na pytanie: „ile osób liczy Państwa rodzina?”. Wyniki przedstawiono w tabeli:
| Liczba osób w rodzinie | Liczba odpowiedzi |
| 2 | 6 |
| x | 12 |
| 5 | 2 |
Średnia liczba osób w rodzinie dla pytanych osób jest równa 3,5. Wtedy liczba  jest równa
jest równa
A) 3 B) 4 C) 1 D) 7
Kwotę 1000 zł wpłacamy do banku na 3 lata. Kapitalizacja odsetek jest dokonywana w tym banku co kwartał, a roczna stopa procentowa wynosi 8%. Po trzech latach otrzymamy kwotę
A) 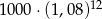 B)
B) 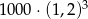 C)
C) 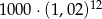 D)
D) 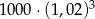
Prostopadłościan dzielimy na części prowadząc dwie płaszczyzny równoległe do jego podstaw, które dzielą krawędź boczną w stosunku 5:1:2. Jaki procent objętości całego prostopadłościanu stanowi objętość najmniejszej z utworzonych części?
A) 15% B) 25% C) 17% D) 12,5%
Zadania otwarte
Rozwiąż równanie 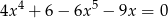 .
.
Podaj przykład liczb całkowitych dodatnich, spełniających nierówność 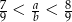 .
.
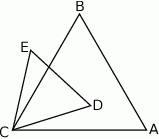
Trójkąty równoboczne 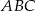 i
i 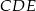 są położone tak, jak na poniższym rysunku. Wykaż, że
są położone tak, jak na poniższym rysunku. Wykaż, że 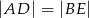 .
.
Jaką wysokość ma romb, jeżeli wiadomo, że jego przekątne mają długości 16 i 30?
Wykaż, że jeżeli 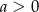 i
i 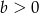 oraz
oraz 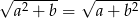 , to
, to 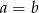 lub
lub 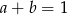 .
.
Rozwiąż nierówność 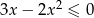 .
.
Wyznacz odległość między prostymi 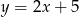 i
i 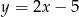 .
.
Dane są trzy sześcienne kostki do gry: czerwona, niebieska i zielona. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że przy jednokrotnym rzucie trzema kostkami liczba otrzymana na niebieskiej kostce jest większa niż suma liczb otrzymanych na dwóch pozostałych kostkach.
Statek płynący z prędkością własną 25 km/h, przepływa odległość z portu 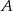 do
do 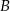 z prądem rzeki w ciągu 40 godzin natomiast drogę powrotną płynąc pod prąd w ciągu 60 godzin. Oblicz średnią prędkość prądu rzeki, oraz odległość między portami
z prądem rzeki w ciągu 40 godzin natomiast drogę powrotną płynąc pod prąd w ciągu 60 godzin. Oblicz średnią prędkość prądu rzeki, oraz odległość między portami 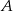 i
i 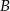 .
.
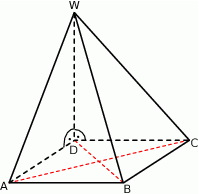
Podstawą ostrosłupa 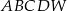 jest kwadrat
jest kwadrat 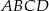 o polu 2. Krawędź boczna
o polu 2. Krawędź boczna 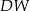 jest wysokością tego ostrosłupa. Długości krawędzi bocznych
jest wysokością tego ostrosłupa. Długości krawędzi bocznych 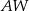 i
i 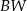 spełniają warunek
spełniają warunek 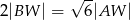 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.