/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 18 kwietnia 2009 Czas pracy: 180 minut
W trójkącie 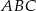 proste zawierające dwusieczne kątów poprowadzonych z wierzchołków
proste zawierające dwusieczne kątów poprowadzonych z wierzchołków 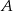 i
i 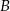 przecinają się pod kątem
przecinają się pod kątem 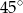 . Wiedząc, że
. Wiedząc, że 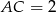 i
i 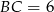 , oblicz
, oblicz
- długość boku
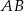 trójkąta
trójkąta 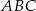 ;
; - długość środkowej trójkąta
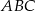 poprowadzonej z wierzchołka
poprowadzonej z wierzchołka 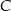 .
.
Wykaż, że jeżeli 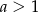 to prawdziwa jest nierówność
to prawdziwa jest nierówność
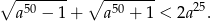
Ania przeczytała książkę science-fiction, która miała 572 strony. Ania każdego dnia czytała o taką samą liczbę stron więcej, niż w dniu poprzednim. Ile dni Ania czytała tę książkę, jeżeli wiadomo, że w trzecim dniu Ania przeczytała 28 stron, a w ostatnim 68?
Wyznacz wszystkie wartości parametru 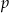 , dla których nierówność
, dla których nierówność 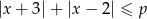 nie ma rozwiązań.
nie ma rozwiązań.
Podstawa trójkąta równoramiennego zawiera się w prostej 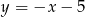 , a jedno z jego ramion w prostej
, a jedno z jego ramion w prostej 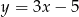 . Wyznacz równanie drugiego ramienia tego trójkąta, jeżeli jednym z jego wierzchołków jest punkt o współrzędnych
. Wyznacz równanie drugiego ramienia tego trójkąta, jeżeli jednym z jego wierzchołków jest punkt o współrzędnych 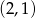 .
.
Rozważmy równanie 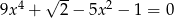 .
.
- Uzasadnij, że równanie to ma 4 pierwiastki.
- Oblicz sumę szóstych potęg wszystkich pierwiastków tego równania.
Ciąg 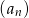 , gdzie
, gdzie 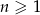 , jest rosnącym ciągiem geometrycznym. Wyznacz największą wartość funkcji
, jest rosnącym ciągiem geometrycznym. Wyznacz największą wartość funkcji 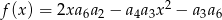 .
.
Podstawą ostrosłupa 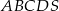 jest kwadrat
jest kwadrat 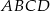 o boku długości 4. Odcinek
o boku długości 4. Odcinek 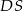 jest wysokością ostrosłupa i ma długość 6. Punkt
jest wysokością ostrosłupa i ma długość 6. Punkt 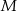 jest środkiem odcinka
jest środkiem odcinka 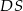 . Oblicz pole przekroju ostrosłupa płaszczyzną
. Oblicz pole przekroju ostrosłupa płaszczyzną 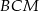 .
.
Losujemy dwie różne liczby całkowite  i
i 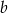 z przedziału
z przedziału 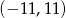 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 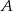 – równanie
– równanie 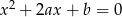 nie ma rozwiązań.
nie ma rozwiązań.
Dana jest funkcja 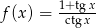 dla
dla 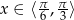 .
.
- Rozwiąż równanie
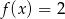 .
. - Wyznacz najmniejszą wartość funkcji
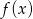 .
.
Długości boków równoległoboku 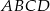 wynoszą 1 i
wynoszą 1 i 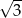 , a kąt przy wierzchołku
, a kąt przy wierzchołku 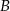 ma miarę
ma miarę 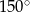 . Oblicz promień okręgu opisanego na trójkącie
. Oblicz promień okręgu opisanego na trójkącie 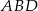 .
.

