/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 27 marca 2010 Czas pracy: 170 minut
Zadania zamknięte
Pierwiastek równania 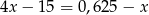 zaokrąglono do wartości 3,2. Błąd względny tego przybliżenia to
zaokrąglono do wartości 3,2. Błąd względny tego przybliżenia to
A) 2,4% B) 2,5% C) 7,5% D) 5%
Liczba 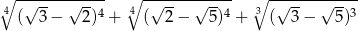 jest równa
jest równa
A) 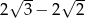 B)
B) 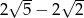 C)
C) 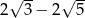 D)
D) 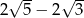
Iloczyn dwóch liczb dodatnich, z których jedna jest o 13 większa od drugiej jest równy 300. Suma tych liczb jest równa
A) 38 B) 13 C) 25 D) 37
Jeżeli 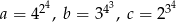 to
to
A) 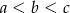 B)
B) 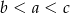 C)
C) 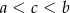 D)
D) 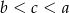
Punkt 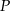 jest punktem wspólnym wykresów funkcji
jest punktem wspólnym wykresów funkcji 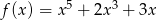 i
i 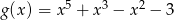 . Zatem suma współrzędnych punktu
. Zatem suma współrzędnych punktu 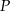
A) jest liczbą większą od 3
B) jest liczbą z przedziału 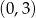
C) jest liczbą naturalną
D) jest liczbą mniejszą od -3
Jeżeli 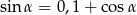 to liczba
to liczba 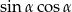 jest równa
jest równa
A) 0,5 B) 0,495 C) 0,99 D) 0,45
Jeżeli 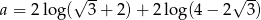 to
to 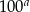 jest liczbą
jest liczbą
A) ujemną B) nieparzystą C) niewymierną D) parzystą
Wykresy funkcji 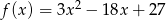 i
i 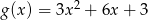 są symetryczne względem prostej
są symetryczne względem prostej
A) 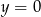 B)
B) 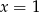 C)
C) 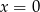 D)
D) 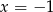
Dwa kolejne wyrazy ciągu geometrycznego 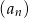 są równe 3 i 18. Wyrazem tego ciągu może być liczba
są równe 3 i 18. Wyrazem tego ciągu może być liczba
A) 27 B) 54 C) 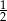 D)
D) 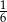
Jeżeli  i
i 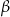 są miarami kątów ostrych trójkąta prostokątnego oraz
są miarami kątów ostrych trójkąta prostokątnego oraz 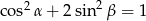 to
to
A) 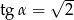 B)
B) 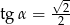 C)
C) 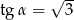 D)
D) 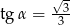
Która z podanych prostych jest symetryczna do prostej 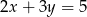 względem osi
względem osi 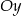 ?
?
A) 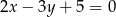 B)
B) 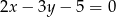 C)
C) 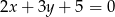 D)
D) 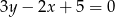
Jeżeli ciąg 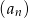 dany jest wzorem
dany jest wzorem 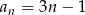 dla
dla 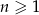 , to suma 10 początkowych wyrazów ciągu
, to suma 10 początkowych wyrazów ciągu 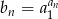 wyraża się wzorem
wyraża się wzorem
A) 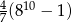 B)
B) 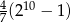 C)
C) 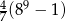 D)
D) 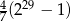
Stopień wielomianu 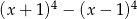 jest równy
jest równy
A) 4 B) 3 C) 2 D) 1
Kąty wewnętrzne przy wierzchołkach 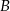 i
i 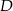 trapezu
trapezu 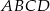 są równe odpowiednio
są równe odpowiednio 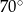 i
i 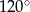 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 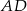 i
i 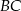 przecinają się pod kątem
przecinają się pod kątem
A) 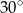 B)
B) 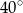 C)
C) 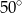 D)
D) 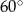
Losujemy jeden wierzchołek i jedną ścianę sześcianu. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowany wierzchołek jest wierzchołkiem wylosowanej ściany jest równe
A) 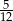 B)
B) 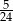 C)
C) 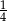 D)
D) 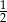
Każdą krawędź graniastosłupa prostego o podstawie będącej sześciokątem skrócono dwukrotnie. W wyniku tej zmiany pole powierzchni graniastosłupa zmniejszyło się o
A) 25% B) 50% C) 75% D) 100%
Która z liczb nie może być równa polu rombu o obwodzie 12?
A) 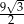 B)
B) 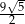 C)
C) 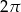 D)
D) 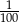
Rozwiązaniem nierówności 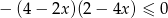 jest zbiór
jest zbiór
A) 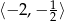 B)
B) 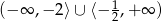 C)
C) 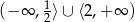 D)
D) 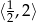
Wykresy funkcji 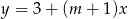 i
i 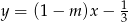 są prostopadłe. Zatem
są prostopadłe. Zatem 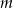
A) jest liczbą niewymierną
B) jest liczbą ujemną
C) jest liczbą naturalną
D) jest liczbą wymierną
Pole sześciokąta foremnego o boku długości 6 jest równe
A) 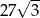 B)
B) 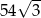 C)
C) 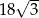 D)
D) 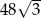
Zadania otwarte
Naszkicuj wykres funkcji
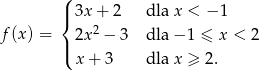
Odczytaj z wykresu maksymalne przedziały monotoniczności funkcji  .
.
Podaj przykład dwóch liczb naturalnych 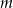 i
i  , które spełniają nierówność
, które spełniają nierówność 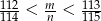 .
.
Wyznacz współrzędne punktu 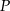 , który dzieli odcinek o końcach
, który dzieli odcinek o końcach 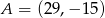 i
i 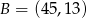 w stosunku
w stosunku 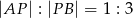 .
.
Stężenie pewnego roztworu wodnego soli wynosi 5%. Ile kilogramów czystej wody należy dodać do 90 kg tego roztworu, aby otrzymać roztwór o stężeniu 2%?
W prostopadłościanie poprowadzono z jednego wierzchołka przekątne ścian bocznych, obie o długości 4. Wiedząc, że kąt między tymi przekątnymi ma miarę 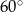 , oblicz pole powierzchni tego prostopadłościanu.
, oblicz pole powierzchni tego prostopadłościanu.
Wyznacz punkty wspólne okręgu 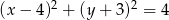 oraz prostej
oraz prostej 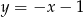 .
.
Wykaż, że dla dowolnych liczb rzeczywistych 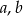 spełniona jest nierówność
spełniona jest nierówność
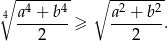
Posługując się wzorem 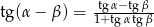 oblicz
oblicz 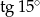 .
.
Prosta równoległa do jednego boku trójkąta dzieli jego pole na połowy. W jakim stosunku prosta ta dzieli pozostałe boki trójkąta?
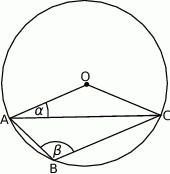
Udowodnij, że jeżeli 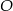 jest środkiem okręgu, na którym leżą punkty
jest środkiem okręgu, na którym leżą punkty 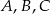 , to
, to 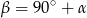 .
.
Sprzedawca kupuje miesięcznie w hurtowni laptopy, płacąc 1200 zł za sztukę. W chwili obecnej sprzedaje 20 laptopów miesięcznie w cenie 1400 zł za sztukę, oraz oszacował, że każda kolejna obniżka ceny o 10 zł zwiększa o 2 liczbę sprzedanych laptopów. Jaką powinien ustalić cenę laptopa, aby jego zysk był największy? Ile jest równy ten maksymalny miesięczny zysk?

