/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki poziom rozszerzony Matura 2008/2009 Informator CKE Czas pracy: 180 minut
Dany jest ciąg 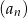 o wyrazie ogólnym
o wyrazie ogólnym 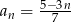 , dla
, dla 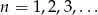 .
.
- Sprawdź, czy ciąg
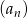 jest arytmetyczny.
jest arytmetyczny. - Oblicz, dla jakiej wartości
 liczby
liczby 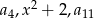 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
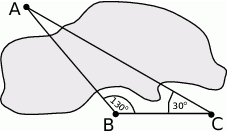
Obiekty 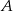 i
i 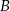 leżą po dwóch stronach jeziora. W terenie dokonano pomiarów odpowiednich kątów i ich wyniki przedstawiono na rysunku. Odległość między obiektami
leżą po dwóch stronach jeziora. W terenie dokonano pomiarów odpowiednich kątów i ich wyniki przedstawiono na rysunku. Odległość między obiektami 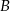 i
i  jest równa 400 m. Oblicz odległość w linii prostej między obiektami
jest równa 400 m. Oblicz odległość w linii prostej między obiektami  i
i  i podaj wynik, zaokrąglając go do jednego metra.
i podaj wynik, zaokrąglając go do jednego metra.
Dana jest funkcja kwadratowa 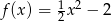 .
.
- Narysuj wykres funkcji
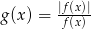 , której dziedziną jest zbiór
, której dziedziną jest zbiór 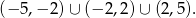
- Zapisz zbiór rozwiązań nierówności
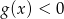 .
.
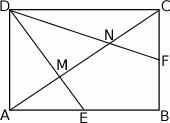
W prostokącie 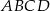 wierzchołek
wierzchołek 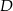 połączono odcinkami ze środkami
połączono odcinkami ze środkami 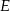 i
i 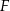 boków
boków 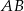 i
i 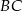 , zaś
, zaś 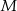 i
i 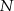 to punkty przecięcia tych odcinków z przekątną
to punkty przecięcia tych odcinków z przekątną 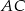 .
.
- Uzasadnij, że odcinki
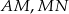 i
i 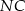 są jednakowej długości.
są jednakowej długości. - Uzasadnij, że trójkąty
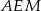 i
i 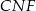 mają równe pola.
mają równe pola.
Dane są punkty 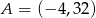 i
i 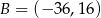 . Wykaż, że koło o średnicy
. Wykaż, że koło o średnicy 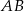 jest zawarte w II ćwiartce prostokątnego układu współrzędnych.
jest zawarte w II ćwiartce prostokątnego układu współrzędnych.
Dany jest wielomian 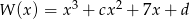 .
.
- Wyznacz wartości współczynników
 i
i 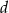 wielomianu
wielomianu 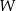 , wiedząc, że jest podzielny przez dwumian
, wiedząc, że jest podzielny przez dwumian 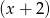 , zaś przy dzieleniu przez dwumian
, zaś przy dzieleniu przez dwumian 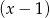 otrzymujemy resztę 3.
otrzymujemy resztę 3. - Dla
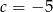 i
i 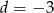 rozwiąż nierówność
rozwiąż nierówność 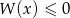 .
.
Wyznacz wszystkie rozwiązania równania 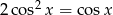 należące do przedziału
należące do przedziału 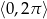 .
.
Dany jest ciąg 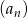 o wyrazie ogólnym
o wyrazie ogólnym 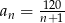 , dla każdej liczby naturalnej
, dla każdej liczby naturalnej 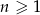 . Ze zbioru liczb
. Ze zbioru liczb 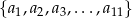 losujemy kolejno, trzy razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno, trzy razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 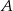 – wylosujemy trzy liczby całkowite, które będą kolejnymi wyrazami ciągu malejącego.
– wylosujemy trzy liczby całkowite, które będą kolejnymi wyrazami ciągu malejącego.
Na okręgu o danym promieniu  opisano trapez równoramienny
opisano trapez równoramienny 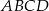 o dłuższej podstawie
o dłuższej podstawie 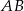 i krótszej
i krótszej 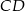 . Punkt styczności
. Punkt styczności 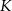 dzieli ramię
dzieli ramię 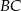 tak, że
tak, że 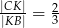 .
.
- Wyznacz długość ramienia tego trapezu.
- Oblicz cosinus kąta
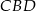 .
.
Dany jest ostrosłup prawidłowy trójkątny, w którym długość krawędzi podstawy jest równa  . Kąt między krawędzią boczną i krawędzią podstawy ma miarę
. Kąt między krawędzią boczną i krawędzią podstawy ma miarę 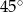 . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
. Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
Ostrokątny trójkąt równoramienny 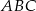 o podstawie
o podstawie 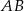 jest wpisany w okrąg o równaniu
jest wpisany w okrąg o równaniu 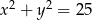 . Punkty
. Punkty 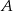 i
i 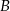 leżą na prostej o równaniu
leżą na prostej o równaniu 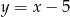 .
.
- Oblicz współrzędne punktów:
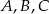 .
. - Oblicz kąty trójkąta
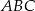 .
.

