/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 24 marca 2018 Czas pracy: 170 minut
Zadania zamknięte
Niech 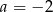 ,
, 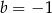 i
i 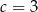 . Wartość wyrażenia
. Wartość wyrażenia 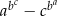 jest równa
jest równa
A) 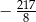 B)
B) 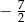 C)
C) 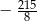 D)
D) 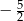
Liczba 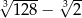 jest równa
jest równa
A) 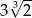 B) 3 C)
B) 3 C) 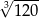 D) 4
D) 4
Kwotę 2000 zł ulokowano w banku na dwuletnią lokatę oprocentowaną w wysokości 8% w stosunku rocznym. Po każdym kwartale środki zgromadzone na lokacie są powiększane o odsetki, od których odprowadzany jest podatek w wysokości 19%. Maksymalna kwota, jaką po upływie dwóch lat będzie można wypłacić z banku, jest równa
A) 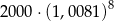 B)
B) 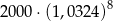 C)
C) 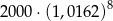 D)
D) 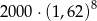
Liczba 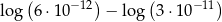 jest równa
jest równa
A) 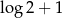 B)
B) 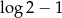 C)
C) 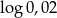 D)
D) 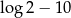
Liczba 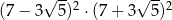 jest równa
jest równa
A) 49 B) 376 C) 16 D) 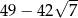
Do zbioru rozwiązań nierówności 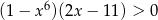 nie należy liczba
nie należy liczba
A) 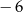 B)
B) 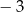 C) 3 D) 6
C) 3 D) 6
Funkcja liniowa określona jest wzorem 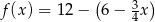 . Miejscem zerowym funkcji
. Miejscem zerowym funkcji 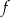 jest
jest
A) 8 B)  C)
C) 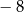 D)
D) 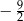
Rozwiązaniem równania 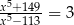 , gdzie
, gdzie 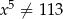 jest liczba należąca do przedziału
jest liczba należąca do przedziału
A) 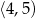 B)
B) 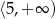 C)
C) 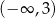 D)
D) 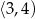
Punkty 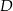 i
i 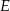 dzielą bok
dzielą bok 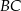 trójkąta
trójkąta 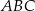 na trzy odcinki, których stosunek długości
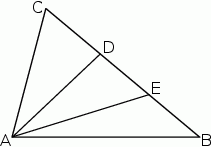
na trzy odcinki, których stosunek długości 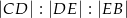 jest równy 8:9:10 (zobacz rysunek). Stosunek pól trójkątów
jest równy 8:9:10 (zobacz rysunek). Stosunek pól trójkątów 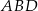 i
i 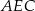 jest równy
jest równy
A)  B)
B) 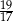 C)
C) 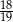 D)
D) 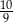
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 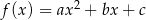 , której miejsca zerowe to:
, której miejsca zerowe to: 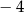 i 2.
i 2.
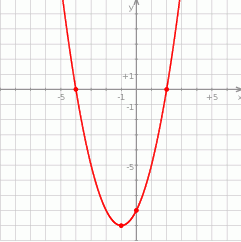
Współczynnik  we wzorze funkcji
we wzorze funkcji 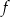 jest równy
jest równy
A) 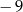 B)
B) 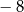 C) 4 D)
C) 4 D) 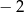
Suma początkowych wyrazów ciągu 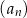 ,
, 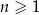 , określona jest wzorem
, określona jest wzorem 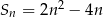 . Trzeci wyraz ciągu
. Trzeci wyraz ciągu 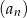 jest równy
jest równy
A) 4 B) 18 C) 6 D) 12
Rysunek przedstawia wykresy funkcji 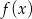 i
i 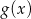 .
.
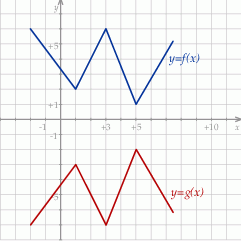
Prawdziwa jest równość:
A) 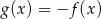 B)
B) 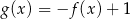 C)
C) 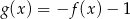 D)
D) 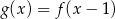
Pole koła wpisanego w trójkąt równoboczny jest równe 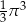 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 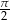 B)
B) 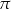 C)
C) 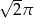 D)
D) 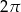
Jeśli 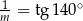 , to
, to
A) 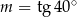 B)
B) 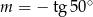 C)
C) 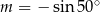 D)
D) 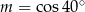
Dany jest ciąg geometryczny 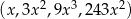 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 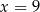 B)
B) 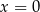 C)
C) 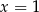 D)
D) 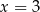
Na okręgu o środku w punkcie 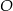 leżą punkty
leżą punkty 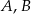 i
i 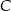 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 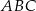 ma miarę
ma miarę 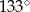 , a kąt
, a kąt 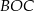 ma miarę
ma miarę 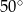 .
.
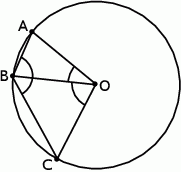
Kąt 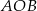 ma miarę
ma miarę
A) 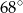 B)
B) 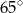 C)
C) 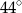 D)
D) 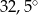
Na rysunku przedstawiona jest prosta 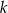 , przechodząca przez punkt
, przechodząca przez punkt 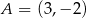 i przez początek układu współrzędnych, oraz zaznaczony jest kąt
i przez początek układu współrzędnych, oraz zaznaczony jest kąt  nachylenia tej prostej do osi
nachylenia tej prostej do osi 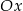 .
.
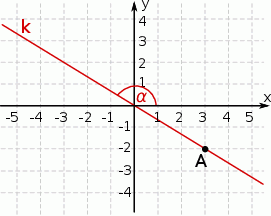
Zatem
A) 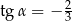 B)
B) 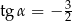 C)
C) 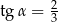 D)
D) 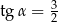
Punkt 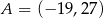 i środek
i środek 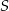 odcinka
odcinka 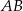 są położone symetrycznie względem początku układu współrzędnych. Zatem punkt
są położone symetrycznie względem początku układu współrzędnych. Zatem punkt 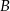 ma współrzędne
ma współrzędne
A) 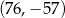 B)
B) 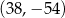 C)
C) 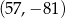 D)
D) 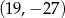
Z pudełka, w którym jest tylko 8 kul białych i  kul czarnych, losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli czarnej jest równe
kul czarnych, losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli czarnej jest równe  . Liczba kul czarnych jest równa
. Liczba kul czarnych jest równa
A) 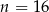 B)
B) 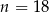 C)
C) 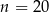 D)
D) 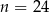
Punkt 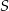 jest środkiem okręgu wpisanego w trójkąt równoramienny
jest środkiem okręgu wpisanego w trójkąt równoramienny 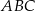 , w którym
, w którym 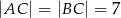 i
i 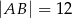 .
.
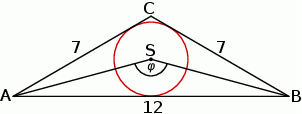
Wówczas miara 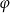 kąta
kąta 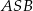 spełnia warunek
spełnia warunek
A) 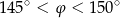 B)
B) 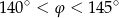 C)
C) 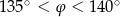 D)
D) 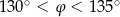
Promień kuli o polu powierzchni równym 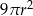 powiększono 2 razy. Objętość tak zmienionej kuli jest równa
powiększono 2 razy. Objętość tak zmienionej kuli jest równa
A) 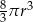 B)
B) 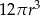 C)
C) 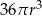 D)
D) 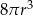
Wysokość 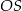 walca jest równa 2, a cosinus kąta
walca jest równa 2, a cosinus kąta 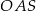 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy  .
.
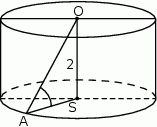
Pole powierzchni bocznej tego walca jest równe
A) 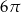 B)
B) 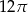 C)
C) 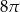 D)
D) 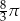
Średnia arytmetyczna zestawu danych:  , 2, 4, 6, 8, 10, 13, 16 jest równa 8,5. Wtedy mediana tego zestawu danych jest równa
, 2, 4, 6, 8, 10, 13, 16 jest równa 8,5. Wtedy mediana tego zestawu danych jest równa
A) 8 B) 8,5 C) 9 D) 10
Suma cyfr najmniejszej sześciocyfrowej liczby naturalnej podzielnej przez 133 jest równa
A) 3 B) 8 C) 7 D) 10
Zadania otwarte
Punkt 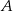 jest punktem wspólnym prostych prostopadłych
jest punktem wspólnym prostych prostopadłych 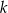 i
i 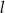 o równaniach
o równaniach 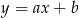 oraz
oraz 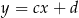 . Wykaż, że jeżeli
. Wykaż, że jeżeli 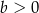 i
i 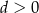 , to druga współrzędna punktu
, to druga współrzędna punktu 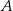 jest liczbą dodatnią.
jest liczbą dodatnią.
Rozwiąż nierówność 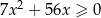 .
.
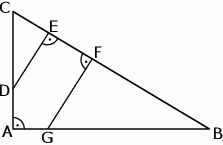
Dany jest trójkąt prostokątny 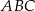 . Na przyprostokątnych
. Na przyprostokątnych 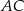 i
i 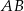 tego trójkąta obrano odpowiednio punkty
tego trójkąta obrano odpowiednio punkty 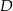 i
i 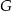 . Na przeciwprostokątnej
. Na przeciwprostokątnej 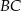 wyznaczono punkty
wyznaczono punkty 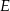 i
i 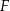 takie, że
takie, że 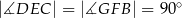 (zobacz rysunek). Wykaż, że trójkąt
(zobacz rysunek). Wykaż, że trójkąt 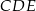 jest podobny do trójkąta
jest podobny do trójkąta  .
.
Dany jest ciąg geometryczny 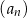 , określony dla
, określony dla 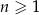 , w którym spełniona jest równość
, w którym spełniona jest równość 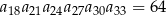 . Oblicz iloczyn
. Oblicz iloczyn 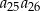 .
.
Wykaż, że prawdziwa jest nierówność 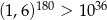 .
.
Ze zbioru liczb 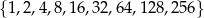 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 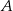 polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą.
polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą.
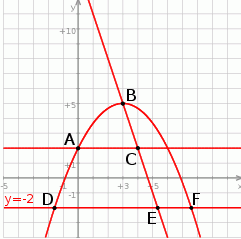
Na rysunku przedstawiono fragmenty wykresów funkcji kwadratowej oraz trzech funkcji liniowych. Zaznaczono również niektóre punkty szczególne tych wykresów: 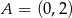 ,
, 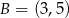 i
i 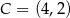 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 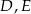 i
i 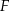 .
.
Przekątne prostokąta 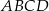 o polu
o polu 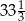 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 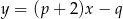 i
i 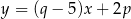 . Ponadto prosta
. Ponadto prosta 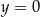 jest osią symetrii tego prostokąta. Oblicz obwód tego prostokąta.
jest osią symetrii tego prostokąta. Oblicz obwód tego prostokąta.
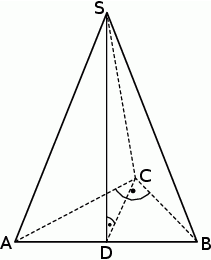
Podstawą ostrosłupa trójkątnego 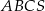 jest trójkąt prostokątny
jest trójkąt prostokątny 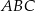 , w którym
, w którym 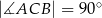 i
i 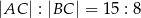 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 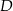 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 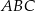 , a odcinek
, a odcinek 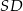 jest wysokością ostrosłupa. Objętość ostrosłupa jest równa 8, a pole ściany
jest wysokością ostrosłupa. Objętość ostrosłupa jest równa 8, a pole ściany 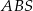 jest równe 17. Oblicz długość krawędzi
jest równe 17. Oblicz długość krawędzi 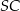 ostrosłupa
ostrosłupa