/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki poziom rozszerzony
(formuła 2015) 12 maja 2023 Czas pracy: 180 minut
Zadania zamknięte
Granica 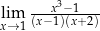 jest równa
jest równa
A) 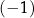 B) 0 C)
B) 0 C) 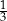 D) 1
D) 1
Dane są wektory ![→ u = [4,− 5]](https://img.zadania.info/zes/0092012/HzesT3x.png) oraz
oraz ![→ v = [− 1,− 5]](https://img.zadania.info/zes/0092012/HzesT4x.png) . Długość wektora
. Długość wektora 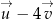 jest równa
jest równa
A) 7 B) 15 C) 17 D) 23
Punkty 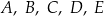 leżą na okręgu o środku
leżą na okręgu o środku 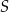 . Miara kąta
. Miara kąta 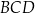 jest równa
jest równa 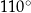 , a miara kąta
, a miara kąta 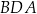 jest równa
jest równa 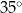 (zobacz rysunek).
(zobacz rysunek).

Wtedy kąt 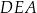 ma miarę równą
ma miarę równą
A) 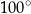 B)
B) 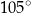 C)
C) 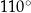 D)
D) 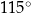
Dany jest zbiór trzynastu liczb 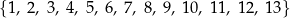 , z którego losujemy jednocześnie dwie liczby. Wszystkich różnych sposobów wylosowania z tego zbioru dwóch liczb, których iloczyn jest liczbą parzystą, jest
, z którego losujemy jednocześnie dwie liczby. Wszystkich różnych sposobów wylosowania z tego zbioru dwóch liczb, których iloczyn jest liczbą parzystą, jest
A) 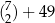 B)
B) 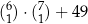 C)
C) 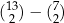 D)
D) 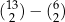
Zadania otwarte
Wielomian 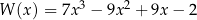 ma dokładnie jeden pierwiastek rzeczywisty. Oblicz ten pierwiastek.
ma dokładnie jeden pierwiastek rzeczywisty. Oblicz ten pierwiastek.
Liczby rzeczywiste  oraz
oraz 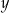 spełniają jednocześnie równanie
spełniają jednocześnie równanie 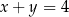 i nierówność
i nierówność
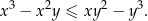
Wykaż, że 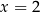 oraz
oraz 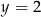 .
.
Dany jest trójkąt prostokątny 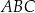 , w którym
, w którym 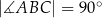 oraz
oraz 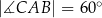 . Punkty
. Punkty 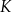 i
i 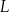 leżą na bokach – odpowiednio –
leżą na bokach – odpowiednio – 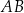 i
i 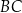 tak, że
tak, że 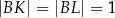 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 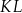 przecina wysokość
przecina wysokość 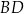 tego trójkąta w punkcie
tego trójkąta w punkcie 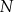 , a ponadto
, a ponadto 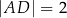 .
.
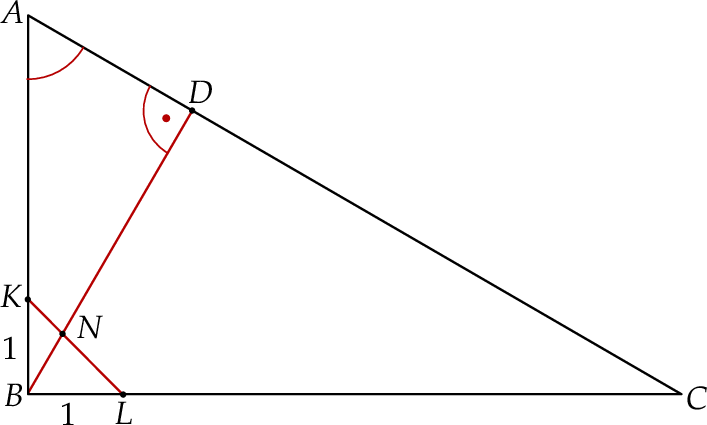
Wykaż, że 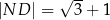 .
.
W pojemniku jest siedem kul: pięć kul białych i dwie kule czarne. Z tego pojemnika losujemy jednocześnie dwie kule bez zwracania. Następnie – z kul pozostałych w pojemniku – losujemy jeszcze jedną kulę. Oblicz prawdopodobieństwo wylosowania kuli czarnej w drugim losowaniu.
Funkcja 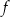 jest określona wzorem
jest określona wzorem 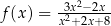 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Punkt
. Punkt 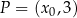 należy do wykresu funkcji
należy do wykresu funkcji 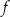 . Oblicz
. Oblicz 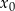 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 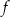 w punkcie
w punkcie 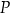 .
.
Rozwiąż nierówność 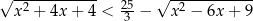 .
.
Określamy kwadraty 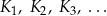 następująco:
następująco:
-
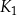 jest kwadratem o boku długości
jest kwadratem o boku długości 
-
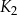 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 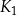 i dzieli ten bok w stosunku 1 : 3
i dzieli ten bok w stosunku 1 : 3 -
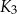 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 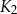 i dzieli ten bok w stosunku 1 : 3
i dzieli ten bok w stosunku 1 : 3
i ogólnie, dla każdej liczby naturalnej 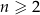 ,
,
-
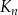 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 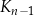 i dzieli ten bok w stosunku 1 : 3.
i dzieli ten bok w stosunku 1 : 3.
Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.
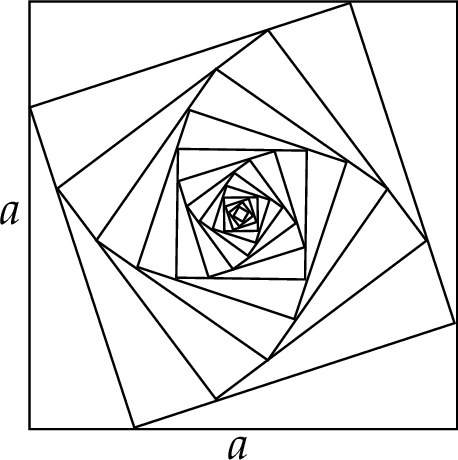
Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu.
Rozwiąż równanie 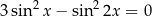 w przedziale
w przedziale ![[π ,2π ]](https://img.zadania.info/zes/0092012/HzesT65x.png) .
.
Czworokąt 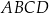 , w którym
, w którym 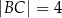 i
i 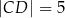 , jest opisany na okręgu. Przekątna
, jest opisany na okręgu. Przekątna 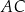 tego czworokąta tworzy z bokiem
tego czworokąta tworzy z bokiem 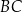 kąt o mierze
kąt o mierze 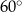 , natomiast z bokiem
, natomiast z bokiem 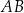 – kąt ostry, którego sinus jest równy
– kąt ostry, którego sinus jest równy  . Oblicz obwód czworokąta
. Oblicz obwód czworokąta 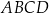 .
.
Dany jest sześcian 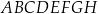 o krawędzi długości 6. Punkt
o krawędzi długości 6. Punkt 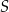 jest punktem przecięcia przekątnych
jest punktem przecięcia przekątnych 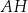 i
i 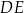 ściany bocznej
ściany bocznej 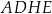 (zobacz rysunek).
(zobacz rysunek).
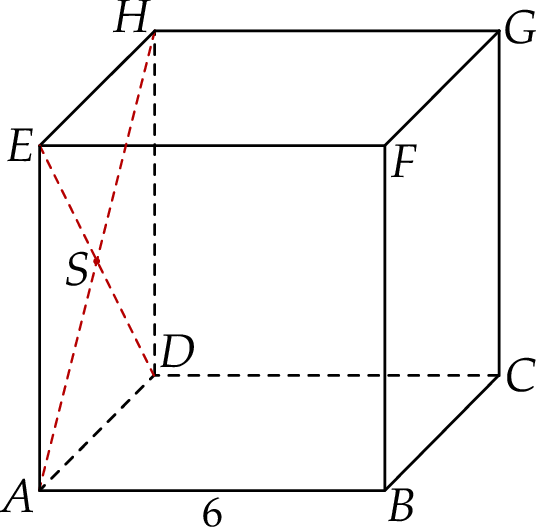
Oblicz wysokość trójkąta 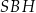 poprowadzoną z punktu
poprowadzoną z punktu 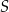 na bok
na bok 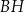 tego trójkąta.
tego trójkąta.
Wyznacz wszystkie wartości parametru 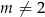 , dla których równanie
, dla których równanie
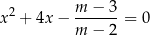
ma dwa różne rozwiązania rzeczywiste 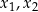 spełniające warunek
spełniające warunek 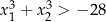 .
.
Rozważamy trójkąty 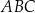 , w których
, w których 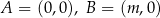 , gdzie
, gdzie 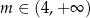 , a wierzchołek
, a wierzchołek 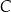 leży na prostej o równaniu
leży na prostej o równaniu 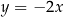 . Na boku
. Na boku 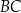 tego trójkąta leży punkt
tego trójkąta leży punkt 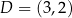 .
.
-
Wykaż, że dla
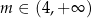 pole
pole 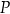 trójkąta
trójkąta 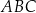 , jako funkcja zmiennej
, jako funkcja zmiennej 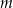 , wyraża się wzorem
, wyraża się wzorem 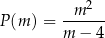
-
Oblicz tę wartość
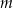 , dla której funkcja
, dla której funkcja 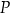 osiąga wartość najmniejszą. Wyznacz równanie prostej
osiąga wartość najmniejszą. Wyznacz równanie prostej 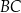 , przy której funkcja
, przy której funkcja 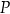 osiąga tę najmniejszą wartość.
osiąga tę najmniejszą wartość.

