/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 29 kwietnia 2023 Czas pracy: 180 minut
Dane są liczby rzeczywiste  i
i 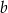 takie, że
takie, że 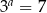 i
i 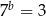 . Wykaż, ze
. Wykaż, ze
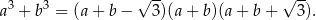
Informacja do zadań 2.1 i 2.2
Dana jest funkcja 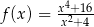 określona dla
określona dla 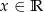 .
.
Udowodnij, że dla każdej liczby rzeczywistej  , spełniona jest nierówność
, spełniona jest nierówność 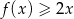 .
.
Wyznacz równania stycznych do wykresu funkcji 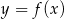 w punktach o rzędnej
w punktach o rzędnej 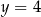 .
.
Maszyna napełnia butelki wodą, przy czym każda butelka ma zostać napełniona wodą do 750 ml objętości. Prawdopodobieństwo tego, że butelka zostanie napełniona prawidłowo wynosi 97%. Kontroli poddano partię 30 butelek napełnionych przez tę maszynę danego dnia. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wśród tych 30 losowo wybranych butelek znajdą się co najwyżej dwie butelki, które nie zostały prawidłowo napełnione.
Pole trójkąta ostrokątnego o bokach 40 i 29 jest równe 420. Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Trapez równoramienny o przekątnej długości 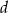 i ramieniu długości
i ramieniu długości  jest opisany na okręgu. Wykaż, że odległość środka okręgu wpisanego w ten trapez od końca krótszej podstawy jest równa
jest opisany na okręgu. Wykaż, że odległość środka okręgu wpisanego w ten trapez od końca krótszej podstawy jest równa 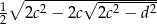 .
.
Dany jest nieskończony ciąg geometryczny 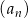 określony dla
określony dla 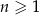 , w którym
, w którym 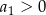 . Suma
. Suma 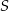 wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność
wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność 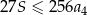 . Wyznacz iloraz tego ciągu.
. Wyznacz iloraz tego ciągu.
Rozwiąż równanie 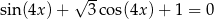 w przedziale
w przedziale 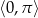 .
.
Wyznacz wszystkie wartości parametru 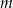 , dla których równanie
, dla których równanie
![(x − 3)[x2 + (m − 9)x + m2 − m + 16] = 0](https://img.zadania.info/zes/0092118/HzesT22x.gif)
ma trzy różne rozwiązania rzeczywiste 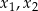 oraz
oraz 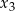 , spełniające warunek
, spełniające warunek
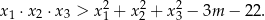
Podstawą ostrosłupa 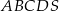 jest równoległobok
jest równoległobok 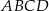 o przekątnej długości
o przekątnej długości 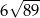 i bokach długości 32 i 34. Pole powierzchni bocznej jednej ze ścian bocznych ostrosłupa jest mniejsze od pola powierzchni sąsiedniej ściany bocznej i jest równe 1808. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych równoległoboku
i bokach długości 32 i 34. Pole powierzchni bocznej jednej ze ścian bocznych ostrosłupa jest mniejsze od pola powierzchni sąsiedniej ściany bocznej i jest równe 1808. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych równoległoboku 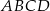 , a jego ściany boczne są trójkątami ostrokątnymi. Oblicz długość krótszej z krawędzi bocznych ostrosłupa
, a jego ściany boczne są trójkątami ostrokątnymi. Oblicz długość krótszej z krawędzi bocznych ostrosłupa 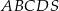 .
.
Maksymalny zbiór, na którym funkcja rzeczywista
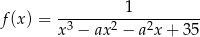
jest rosnąca jest jedyny i jest niepustym przedziałem postaci 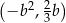 , dla pewnej liczby całkowitej
, dla pewnej liczby całkowitej 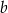 . Wyznacz dziedzinę funkcji
. Wyznacz dziedzinę funkcji 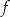 oraz jej największą wartość na przedziale
oraz jej największą wartość na przedziale ![[− 2,3]](https://img.zadania.info/zes/0092118/HzesT35x.gif) .
.
Prosta o równaniu 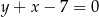 zawiera jedną z dwusiecznych kątów wewnętrznych trójkąta
zawiera jedną z dwusiecznych kątów wewnętrznych trójkąta 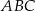 , w którym
, w którym 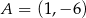 i
i 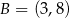 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.

