/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 22 marca 2014 Czas pracy: 180 minut
Prosta 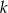 równoległa do osi
równoległa do osi 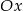 przecina wykres funkcji
przecina wykres funkcji 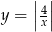 w dwóch punktach
w dwóch punktach 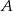 i
i 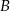 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 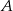 i
i 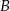 jeżeli wiadomo, że razem z punktem
jeżeli wiadomo, że razem z punktem 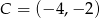 tworzą trójkąt o polu 6.
tworzą trójkąt o polu 6.
Wielomiany 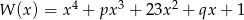 oraz
oraz 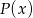 są wielomianami o współczynnikach całkowitych, przy czym
są wielomianami o współczynnikach całkowitych, przy czym ![2 W (x ) = [P (x)]](https://img.zadania.info/zes/0092169/HzesT10x.gif) . Wyznacz wszystkie możliwe wartości
. Wyznacz wszystkie możliwe wartości 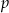 i
i 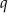 .
.
Rozwiąż równanie 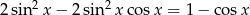 w przedziale
w przedziale 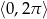 .
.
Rozwiąż nierówność 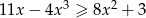 .
.
Dane są punkty 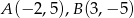 . Punkt
. Punkt 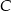 należy do okręgu o równaniu
należy do okręgu o równaniu 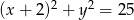 . Znajdź współrzędne punktu
. Znajdź współrzędne punktu 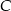 tak, aby pole trójkąta
tak, aby pole trójkąta 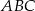 było największe. Oblicz to pole.
było największe. Oblicz to pole.
Wielomian 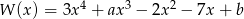 jest podzielny przez dwumian
jest podzielny przez dwumian 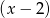 , a przy dzieleniu przez
, a przy dzieleniu przez 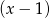 daje resztę 3. Wyznacz
daje resztę 3. Wyznacz  i
i 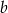 .
.
W trójkącie prostokątnym 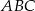 dwusieczna kąta prostego przecina przeciwprostokątną
dwusieczna kąta prostego przecina przeciwprostokątną 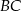 w punkcie
w punkcie 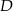 . Środek okręgu wpisanego w ten trójkąt dzieli odcinek
. Środek okręgu wpisanego w ten trójkąt dzieli odcinek 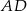 w stosunku
w stosunku 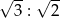 , licząc od punktu
, licząc od punktu 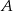 . Oblicz miary kątów ostrych trójkąta
. Oblicz miary kątów ostrych trójkąta 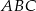 .
.
Liczby 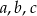 mają tę własność, że każdy z ciągów:
mają tę własność, że każdy z ciągów: 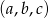 ,
, 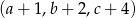 i
i 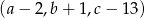 jest ciągiem geometrycznym. Oblicz
jest ciągiem geometrycznym. Oblicz 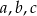 .
.
Czworokąt 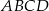 jest trapezem prostokątnym, w którym
jest trapezem prostokątnym, w którym 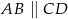 . Wykaż że
. Wykaż że
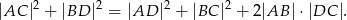
Do windy na parterze budynku wsiadło 6 osób, po czym każda z nich w sposób losowy wysiadła na jednym z trzech pięter budynku. Jakie jest prawdopodobieństwo, że na żadnym z pięter nie wysiadły więcej niż 4 osoby?
W ostrosłup prawidłowy czworokątny wpisano sześcian tak, że jego cztery wierzchołki należą do krawędzi bocznych ostrosłupa, a pozostałe do płaszczyzny podstawy. Oblicz długość krawędzi sześcianu, jeżeli wysokość ostrosłupa jest równa 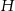 , a długość jego krawędzi podstawy jest równa
, a długość jego krawędzi podstawy jest równa  .
.

