/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 19 marca 2016 Czas pracy: 170 minut
Zadania zamknięte
Liczba 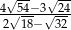 jest równa
jest równa
A) 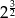 B)
B) 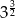 C)
C) 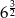 D)
D) 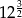
Kwiatek z doniczką kosztował 50 zł, ale doniczka zdrożała o 20%, a kwiatek zdrożał o 10%. Jeżeli nowa cena kwiatka z doniczką wynosi 58,5 złotego, to aktualna cena doniczki to
A) 42 B) 38,5 C) 35 D) 35,5
Dane są liczby: 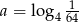 ,
, 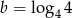 ,
, 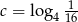 . Który z poniższych warunków jest prawdziwy?
. Który z poniższych warunków jest prawdziwy?
A) 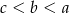 B)
B) 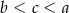 C)
C) 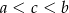 D)
D) 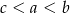
Równość 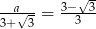 zachodzi dla
zachodzi dla
A) 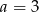 B)
B) 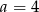 C)
C) 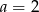 D)
D) 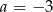
Liczba 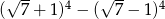 jest równa
jest równa
A) 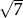 B)
B) 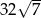 C)
C) 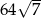 D) 2
D) 2
Równanie 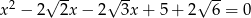
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
Punkt 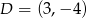 jest obrazem punktu
jest obrazem punktu 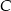 w symetrii względem punktu
w symetrii względem punktu 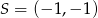 , a punkt
, a punkt 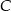 jest środkiem odcinka
jest środkiem odcinka 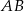 , gdzie
, gdzie 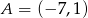 . Punkt
. Punkt 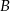 ma współrzędne
ma współrzędne
A) 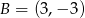 B)
B) 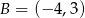 C)
C) 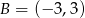 D)
D) 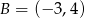
W trójkącie 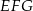 bok
bok 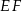 ma długość 24. Prosta równoległa do boku
ma długość 24. Prosta równoległa do boku 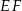 przecina boki
przecina boki 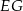 i
i 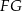 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 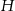 oraz
oraz 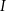 (zobacz rysunek) w taki sposób, że
(zobacz rysunek) w taki sposób, że 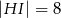 i
i 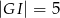 . Wtedy długość odcinka
. Wtedy długość odcinka 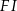 jest równa
jest równa
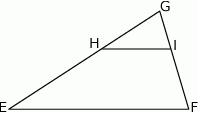
A) 6 B) 9 C) 10 D) 12
Na rysunku przedstawiono wykres funkcji 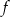 .
.
Zbiorem wartości funkcji 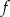 jest
jest
A) 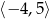 B)
B) 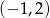 C)
C) 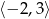 D)
D) 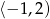
Rozwiązaniem równania 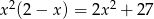 jest
jest
A) 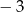 B)
B) 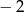 C) 3 D) 2
C) 3 D) 2
Prosta 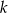 przecina oś
przecina oś 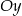 układu współrzędnych w punkcie
układu współrzędnych w punkcie 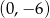 i jest równoległa do prostej o równaniu
i jest równoległa do prostej o równaniu 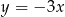 . Wówczas prosta
. Wówczas prosta 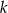 przecina oś
przecina oś 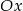 układu współrzędnych w punkcie
układu współrzędnych w punkcie
A) 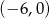 B)
B) 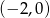 C)
C) 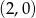 D)
D) 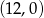
Parabola o wierzchołku 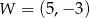 i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem
i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem
A) 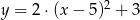
B) 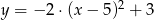
C) 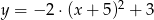
D) 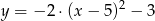
Nierówność 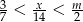 jest spełniona przez dokładnie 14 liczb całkowitych
jest spełniona przez dokładnie 14 liczb całkowitych  . Liczba
. Liczba 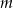 może być równa
może być równa
A) 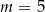 B)
B) 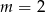 C)
C) 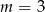 D)
D) 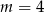
Objętość ostrosłupa prawidłowego czworokątnego jest równa 363, a krawędź podstawy tego ostrosłupa ma długość 11. Wysokość tego ostrosłupa jest równa
A) 3 B) 9 C) 27 D) 108
Suma pierwszego i siódmego wyrazu pewnego ciągu arytmetycznego jest równa 17 . Wynika stąd, że suma trzeciego i piątego wyrazu tego ciągu jest równa
A) 7 B) 16 C) 17 D) 6
Ciąg geometryczny określony jest wzorem 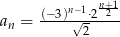 , dla
, dla 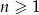 . Czwarty wyraz tego ciągu jest równy
. Czwarty wyraz tego ciągu jest równy
A) 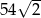 B)
B) 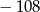 C)
C) 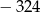 D)
D) 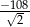
Miara kąta wpisanego w okrąg jest o 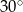 mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
A) 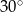 B)
B) 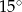 C)
C) 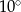 D)
D) 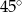
Wartość wyrażenia 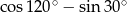 jest równa
jest równa
A) 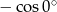 B)
B) 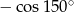 C)
C) 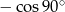 D)
D) 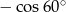
Pole czworokąta przedstawionego na rysunku jest równe
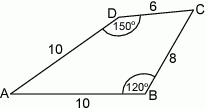
A) 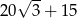 B)
B) 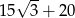 C)
C) 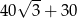 D)
D) 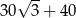
Ze zbioru kolejnych liczb naturalnych 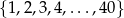 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
A) 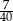 B)
B) 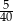 C)
C) 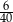 D)
D) 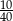
Średnia arytmetyczna zestawu danych: 3, 5, 6, 7, 9 jest taka sama jak średnia arytmetyczna zestawu danych: 3, 5, 6, 8, 9,  . Wynika stąd, że
. Wynika stąd, że
A) 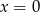 B)
B) 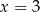 C)
C) 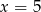 D)
D) 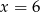
Graniastosłup o podstawie dziewięciokąta ma dokładnie
A) 16 wierzchołków. B) 18 wierzchołków. C) 24 krawędzie. D) 18 krawędzi.
Ile jest wszystkich liczb pięciocyfrowych, większych 43080, utworzonych wyłącznie z cyfr 1, 2, 3, 4 przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane?
A) 48 B) 15 C) 128 D) 192
Przekątna przekroju osiowego walca, którego promień podstawy jest równy 6 i wysokość jest równa 9, ma długość
A) 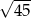 B) 15 C)
B) 15 C) 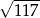 D) 10
D) 10
Zadania otwarte
Rozwiąż nierówność 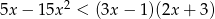 .
.
Wykaż, że dla wszystkich liczb rzeczywistych 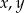 prawdziwa jest nierówność
prawdziwa jest nierówność 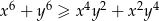 .
.
Przekątna 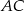 czworokąta
czworokąta 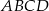 wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że
wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że 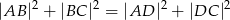 .
.
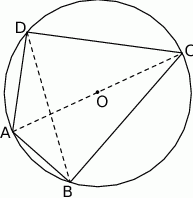
Dane są dwa podzbiory zbioru liczb całkowitych:
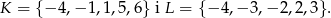
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni.
W układzie współrzędnych są dane punkty 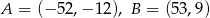 . Prosta
. Prosta 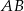 przecina oś
przecina oś 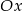 w punkcie
w punkcie 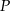 . Oblicz pierwszą współrzędną punktu
. Oblicz pierwszą współrzędną punktu 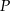 .
.
Ania bawi się sześciennymi klockami o krawędzi 2 cm i buduje z nich bryły w kształcie prostokątów (prostopadłościanów o wysokości 1 klocka) w sposób przedstawiony na poniższym rysunku.
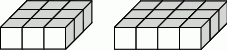
Najpierw Ania zbudowała z klocków pełen kwadrat o krawędzi 36 cm i wykorzystała do tego wszystkie swoje klocki. Następnie zburzyła tę budowlę i ułożyła z tych klocków prostokąt. Wtedy okazało się, że został jej dokładnie jeden klocek, którego nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej pierwszej z ułożonych figur do pola powierzchni całkowitej drugiej figury.
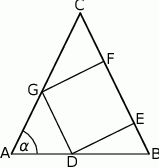
Sinus kąta 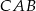 trójkąta równoramiennego
trójkąta równoramiennego 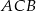 jest równy
jest równy  . Pole kwadratu
. Pole kwadratu 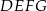 , wpisanego w ten trójkąt (zobacz rysunek), jest równe 4. Oblicz pole trójkąta
, wpisanego w ten trójkąt (zobacz rysunek), jest równe 4. Oblicz pole trójkąta 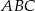 .
.
Trzy liczby tworzą ciąg arytmetyczny. Ich suma jest równa 60. Jeśli pierwszą i trzecią liczbę pozostawimy bez zmian, a drugą pomniejszymy o cztery, to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Oblicz wyrazy ciągu arytmetycznego.
Funkcja kwadratowa 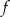 określona jest wzorem
określona jest wzorem 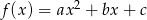 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 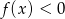 jest przedział
jest przedział 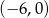 . Najmniejsza wartość funkcji
. Najmniejsza wartość funkcji 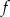 jest równa
jest równa 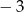 . Oblicz współczynniki
. Oblicz współczynniki 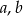 i
i  funkcji
funkcji 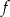 .
.

