/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 12 marca 2016 Czas pracy: 170 minut
Zadania zamknięte
Wskaż rysunek, na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności 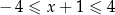 .
.
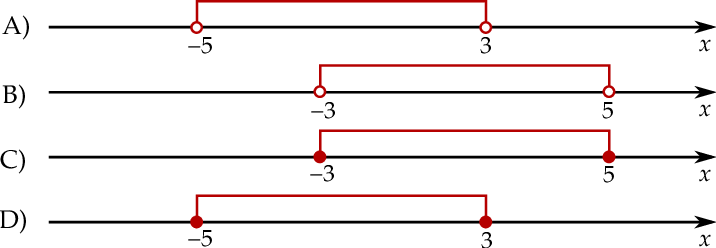
Jeśli 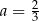 i
i 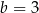 , to wartość wyrażenia
, to wartość wyrażenia 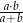 jest równa
jest równa
A) 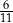 B) 1 C)
B) 1 C)  D)
D) 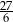
Koszt brutto wysłania SMS-a w usłudze Premium SMS wynosi 17,22 zł. Jaka jest wartość netto tego SMS-a, jeżeli koszt SMS-a obciążony jest 19% podatkiem dochodowym oraz 23% podatkiem VAT?
A) 7,12 zł B) 10,74 zł C) 25,20 zł D) 11,76 zł
Liczba 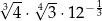 jest równa
jest równa
A) 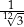 B)
B) 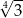 C) 1 D)
C) 1 D) 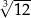
Układ równań 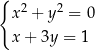 opisuje w układzie współrzędnych na płaszczyźnie
opisuje w układzie współrzędnych na płaszczyźnie
A) zbiór pusty. B) dokładnie jeden punkt.
C) dokładnie dwa różne punkty. D) zbiór nieskończony.
Liczba 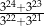 jest równa
jest równa
A) 1 B) 3 C) 6 D) 9
Jeżeli wiadomo, że 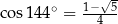 , to
, to
A) 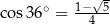 B)
B) 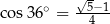 C)
C) 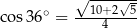 D)
D) 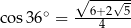
Do zbioru rozwiązań nierówności 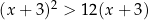 należy liczba
należy liczba
A) 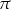 B)
B) 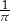 C)
C) 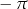 D)
D) 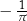
Do wykresu funkcji liniowej określonej wzorem 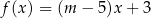 należy punkt
należy punkt 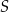 o obu współrzędnych nieparzystych. Liczba
o obu współrzędnych nieparzystych. Liczba 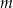 może być równa
może być równa
A) 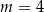 B)
B) 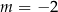 C)
C) 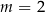 D)
D) 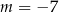
Funkcja 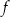 jest określona wzorem
jest określona wzorem 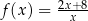 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 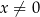 . Wówczas wartość funkcji
. Wówczas wartość funkcji 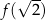 jest równa
jest równa
A) 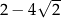 B)
B) 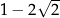 C)
C) 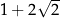 D)
D) 
Równanie 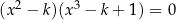 nie ma rozwiązań niewymiernych. Liczba
nie ma rozwiązań niewymiernych. Liczba 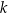 może być równa
może być równa
A) 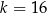 B)
B) 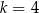 C)
C) 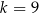 D)
D) 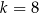
Pierwsza współrzędna wierzchołka paraboli o równaniu 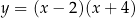 jest równa
jest równa
A) 8 B) 4 C) 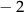 D)
D) 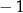
W rosnącym ciągu geometrycznym 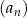 , określonym dla
, określonym dla 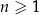 , spełniony jest warunek
, spełniony jest warunek 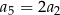 . Iloraz
. Iloraz 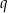 tego ciągu jest równy
tego ciągu jest równy
A) 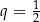 B)
B) 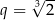 C)
C) 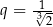 D)
D) 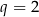
Wszystkie trzycyfrowe liczby naturalne podzielne przez 7 tworzą rosnący ciąg arytmetyczny. Setnym wyrazem tego ciągu jest liczba
A) 791 B) 700 C) 805 D) 798
Długość boku, długość przekątnej oraz pole kwadratu są kolejnymi wyrazami ciągu geometrycznego. Pierwszy wyraz tego ciągu jest
A) liczbą niewymierną B) liczbą całkowitą
C) liczbą z przedziału 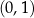 D) wymierną niecałkowitą
D) wymierną niecałkowitą
Promień okręgu wpisanego w trójkąt równoboczny jest o 1 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 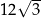 B)
B) 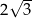 C)
C) 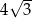 D)
D) 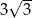
Sinusy dwóch kątów ostrych trójkąta są odpowiednio równe 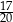 i
i 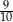 . Jeżeli
. Jeżeli  jest miarą najmniejszego kąta tego trójkąta, to
jest miarą najmniejszego kąta tego trójkąta, to
A) 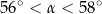 B)
B) 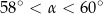 C)
C) 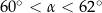 D)
D) 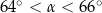
Długości boków trójkąta są liczbami całkowitymi. Jeden bok ma 4 cm, a drugi ma 9 cm. Trzeci bok tego trójkąta może mieć długość
A) 4 cm B) 5 cm C) 14 cm D) 9 cm
W okręgu o środku 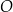 dany jest kąt o mierze
dany jest kąt o mierze 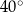 , zaznaczony na rysunku.
, zaznaczony na rysunku.
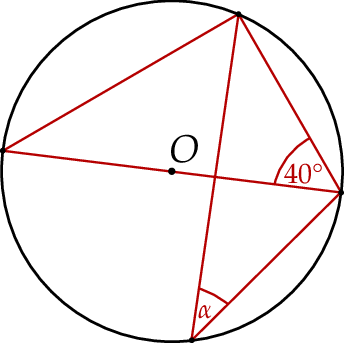
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 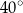 B)
B) 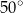 C)
C) 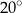 D)
D) 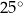
Punkt 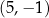 należy do prostej
należy do prostej 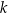 , której współczynnik kierunkowy jest równy
, której współczynnik kierunkowy jest równy 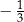 . Wskaż punkt, który nie należy do prostej
. Wskaż punkt, który nie należy do prostej 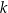 .
.
A) 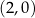 B)
B) 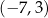 C)
C) 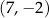 D)
D) 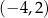
W graniastosłupie prawidłowym czworokątnym 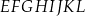 wierzchołki
wierzchołki 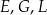 połączono odcinkami (tak jak na rysunku).
połączono odcinkami (tak jak na rysunku).
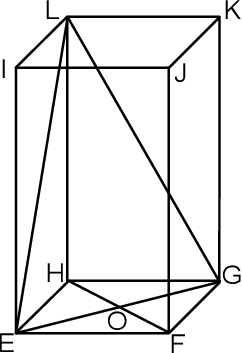
Wskaż kąt między wysokością 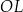 trójkąta
trójkąta 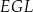 i krawędzią boczną tego graniastosłupa.
i krawędzią boczną tego graniastosłupa.
A) 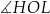 B)
B) 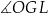 C)
C) 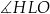 D)
D) 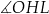
Dany jest trójkąt prostokątny o długościach boków 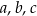 , gdzie
, gdzie 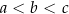 . Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt 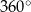 , otrzymujemy bryłę, której pole powierzchni całkowitej jest równe
, otrzymujemy bryłę, której pole powierzchni całkowitej jest równe
A) 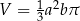 B)
B) 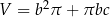 C)
C) 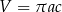 D)
D) 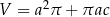
Czterech przyjaciół zarejestrowało spółkę. Wysokość udziałów poszczególnych wspólników w kapitale zakładowym spółki wyraża stosunek 12 : 8 : 3 : 2. Jaką część kapitału zakładowego stanowi udział najmniejszego inwestora?
A) 2% B) 4% C) 6% D) 8%
Ile jest wszystkich liczb naturalnych dwucyfrowych podzielnych przez 14 i niepodzielnych przez 4?
A) 4 B) 6 C) 5 D) 7
W każdym z czterech pojemników znajduje się para kul, z których jedna jest czerwona, a druga – niebieska. Z każdego pojemnika losujemy jedną kulę. Niech 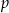 oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z czterech wylosowanych kul będą niebieskie. Wtedy
oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z czterech wylosowanych kul będą niebieskie. Wtedy
A) 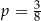 B)
B) 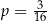 C)
C) 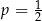 D)
D) 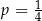
Zadania otwarte
Rozwiąż nierówność 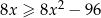 .
.
Rozwiąż równanie 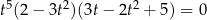 .
.
Wiedząc, że 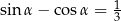 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 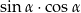 .
.
Wyznacz najmniejszą i największą wartość funkcji kwadratowej 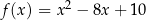 w przedziale
w przedziale 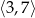 .
.
Oblicz miarę kąta ostrego, którego ramiona są zawarte w prostych o równaniach 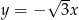 i
i 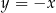 .
.
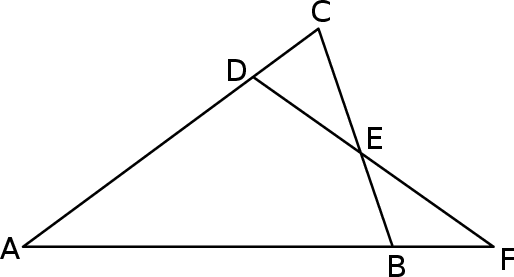
Dany jest trójkąt 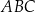 , w którym
, w którym 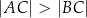 . Na bokach
. Na bokach 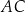 i
i 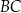 tego trójkąta obrano odpowiednio takie punkty
tego trójkąta obrano odpowiednio takie punkty 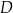 i
i 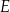 , że zachodzi równość
, że zachodzi równość 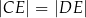 . Proste
. Proste 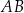 i
i 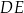 przecinają się w punkcie
przecinają się w punkcie 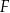 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 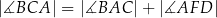 .
.
Dany jest trójkąt równoramienny 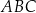 , w którym
, w którym 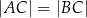 . Ponadto wiadomo, że
. Ponadto wiadomo, że 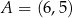 i
i 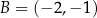 . Wierzchołek
. Wierzchołek 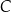 należy do osi
należy do osi 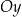 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 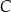 .
.
Objętość ostrosłupa prawidłowego trójkątnego 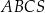 jest równa
jest równa 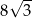 . Długość krawędzi
. Długość krawędzi 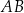 podstawy ostrosłupa jest równa 4 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.
podstawy ostrosłupa jest równa 4 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.
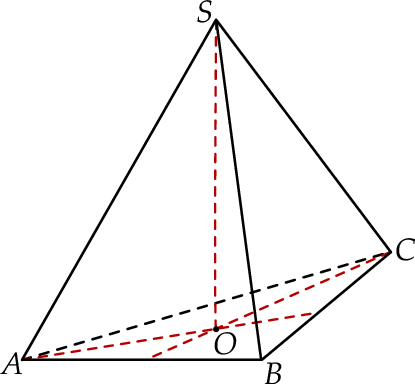
W pewnej szkole podstawowej 123 uczniów klas szóstych ma do dyspozycji 3 rodzaje zajęć dodatkowych: kółko matematyczne, kółko humanistyczne i kółko przyrodnicze. W poniższej tabeli przedstawiono informacje o liczbie uczniów uczęszczających na wybrane rodzaje zajęć.
| Rodzaj zajęć | Liczba uczniów |
| matematyczne | 24 |
| przyrodnicze | 18 |
| humanistyczne | 20 |
| matematyczne i przyrodnicze | 4 |
| matematyczne i humanistyczne | 5 |
| przyrodnicze i humanistyczne | 6 |
| przyrodnicze, humanistyczne i matematyczne | 3 |
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrany uczeń klasy szóstej uczęszcza tylko na jedne zajęcia pozalekcyjne. Wynik przedstaw w formie nieskracalnego ułamka.

