/Szkoła średnia/Zadania maturalne

Optymalizacja – planimetria poziom rozszerzony

Zadanie 1

Oblicz jakie długości powinny mieć boki prostokąta o polu równym 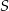S , aby jego przekątna miała najmniejszą możliwą długość. Oblicz długość tej przekątnej.

Zadanie 2

Rozpatrujemy wszystkie trójkąty prostokątne 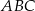ABC o przeciwprostokątnej 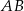AB i obwodzie równym 4. Niech x = |AC | .

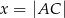  • Wykaż, że pole 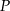P trójkąta 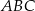ABC jako funkcja zmiennej x jest określone wzorem
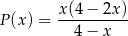
    x(4 − 2x) P(x) = ---------- 4− x
  • Wyznacz dziedzinę funkcji P .
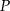  • Oblicz długości boków tego z rozpatrywanych trójkątów, który ma największe pole. Oblicz to największe pole.

Zadanie 3

Rozpatrujemy wszystkie trapezy równoramienne, w które można wpisać okrąg, spełniające warunek: suma długości dłuższej podstawy a i wysokości trapezu jest równa 2.

  • Wyznacz wszystkie wartości a , dla których istnieje trapez o podanych własnościach.
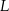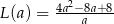
  • Wykaż, że obwód L takiego trapezu, jako funkcja długości a dłuższej podstawy trapezu, wyraża się wzorem 4a2−8a+8 L(a) = a
  • Oblicz tangens kąta ostrego tego spośród rozpatrywanych trapezów, którego obwód jest najmniejszy.

Zadanie 4

Okno na poddaszu ma mieć kształt trapezu równoramiennego, którego przekątna ma długość 6 dm. Oblicz, jakie jest największe możliwe pole powierzchni tego okna.

Zadanie 5

Okno na poddaszu ma mieć kształt trapezu równoramiennego, którego krótsza podstawa i ramiona mają długość po 4 dm. Oblicz, jaką długość powinna mieć dłuższa podstawa tego trapezu, aby do pomieszczenia wpadało przez to okno jak najwięcej światła, czyli aby pole powierzchni okna było największe. Oblicz to pole.

Wersja PDF
Rozwiązania