/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 2 marca 2013 Czas pracy: 170 minut
Zadania zamknięte
Stężenie roztworu początkowo wzrosło o 30%, a po 10 minutach wzrosło o dalsze 20%. W wyniku tych zmian stężenie wzrosło o
A) 44% B) 50% C) 56% D) 60%
Równość 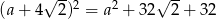 zachodzi dla
zachodzi dla
A) 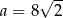 B)
B) 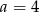 C)
C) 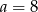 D)
D) 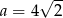
Połową odwrotności sześcianu liczby 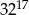 jest
jest
A) 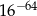 B)
B) 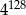 C)
C) 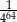 D)
D) 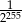
Wskaż 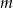 , dla którego miejsce zerowe funkcji liniowej
, dla którego miejsce zerowe funkcji liniowej 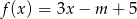 jest liczbą z przedziału
jest liczbą z przedziału 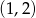 .
.
A) 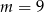 B)
B) 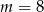 C)
C) 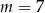 D)
D) 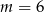
Wskaż liczbę, która spełnia równanie 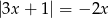 .
.
A) 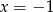 B)
B) 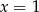 C)
C) 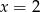 D)
D) 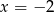
Na jednym z poniższych rysunków przedstawiono fragment wykresu funkcji 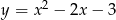 . Wskaż ten rysunek.
. Wskaż ten rysunek.
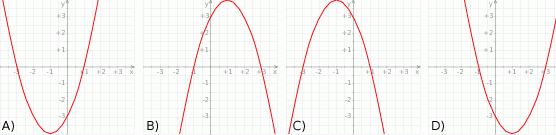
Wyrażenie 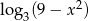 jest określone dla wszystkich liczb
jest określone dla wszystkich liczb  spełniających warunek
spełniających warunek
A) 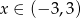 B)
B) 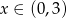 C)
C) 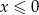 D)
D) 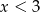
Zbiorem rozwiązań nierówności 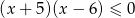 jest
jest
A) 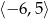
B) 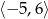
C) 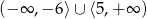
D) 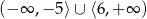
Wskaż wykres funkcji, która w przedziale 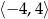 ma dokładnie dwa miejsca zerowe.
ma dokładnie dwa miejsca zerowe.
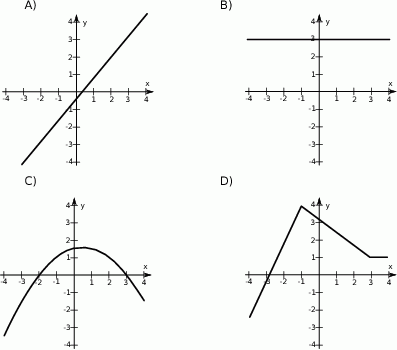
Jeżeli 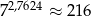 to przybliżona wartość liczby
to przybliżona wartość liczby 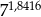 jest równa
jest równa
A) 6 B) 36 C) 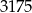 D) 1296
D) 1296
Punkt 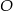 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany 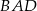 ma miarę
ma miarę
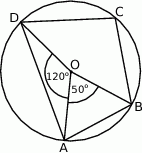
A) 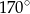 B)
B) 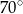 C)
C) 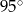 D)
D) 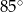
Punkt 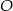 jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
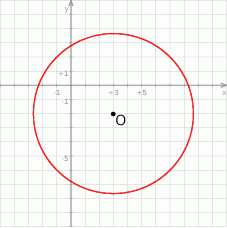
A) 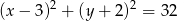
B) 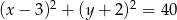
C) 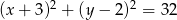
D) 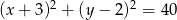
W trójkącie prostokątnym o polu 15 najkrótszy bok ma długość 3. Obwód tego trójkąta jest równy
A) 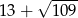 B)
B) 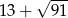 C)
C) 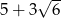 D)
D) 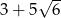
Ciąg 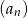 spełnia warunek
spełnia warunek 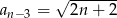 dla
dla 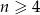 . Wówczas
. Wówczas
A) 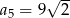 B)
B) 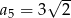 C)
C) 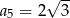 D)
D) 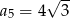
Pole prostokąta jest równe 48. Stosunek długości jego boków jest równy 3:4. Dłuższy bok tego prostokąta ma długość
A) 10 B) 8 C) 7 D) 6
Kąt  jest kątem ostrym i
jest kątem ostrym i 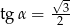 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 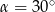 B)
B) 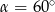 C)
C) 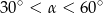 D)
D) 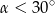
Miary kątów czworokąta tworzą ciąg geometryczny o ilorazie 2. Największy kąt tego czworokąta ma miarę
A) 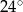 B)
B) 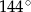 C)
C) 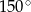 D)
D) 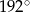
Długość boku trójkąta równobocznego jest równa 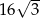 . Promień okręgu wpisanego w ten trójkąt jest równy
. Promień okręgu wpisanego w ten trójkąt jest równy
A) 4 B) 8 C) 12 D) 24
Pan Henryk szykując się rano do pracy wybiera jeden spośród swoich 10 zegarków oraz dwa spośród 18 wiecznych piór, przy czym jedno z nich traktuje jako pióro zapasowe. Na ile sposobów może wybrać zestaw składający się z zegarka i dwóch piór, głównego i zapasowego?
A) 45 B) 46 C) 3240 D) 3060
Przekrój osiowy stożka jest równoramiennym trójkątem prostokątnym o przyprostokątnej długości  . Objętość tego stożka wyraża się wzorem
. Objętość tego stożka wyraża się wzorem
A) 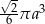 B)
B) 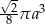 C)
C) 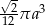 D)
D) 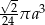
Wskaż równanie prostej równoległej do prostej o równaniu 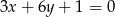 .
.
A) 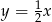 B)
B) 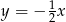 C)
C) 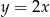 D)
D) 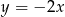
Stosunek objętości dwóch sześcianów jest równy 1 : 125. Zatem stosunek długości krawędzi tych sześcianów wynosi:
A) 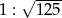 B) 1:125 C) 1:25 D) 1:5
B) 1:125 C) 1:25 D) 1:5
Średnia arytmetyczna cen ośmiu akcji na giełdzie jest równa 600 zł. Za siedem z tych akcji zapłacono 4200 zł. Cena ósmej akcji jest równa
A) 400 zł B) 500 zł C) 600 zł D) 700 zł
Zadania otwarte
Rozwiąż nierówność 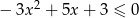 .
.
Punkty 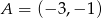 i
i 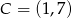 są przeciwległymi wierzchołkami rombu
są przeciwległymi wierzchołkami rombu 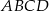 . Wyznacz równanie przekątnej
. Wyznacz równanie przekątnej 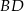 tego rombu.
tego rombu.
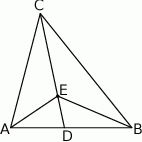
Na dwusiecznej 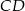 trójkąta
trójkąta 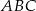 , w którym
, w którym 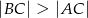 wybrano punkt
wybrano punkt 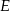 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 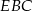 jest większe od pola trójkąta
jest większe od pola trójkąta 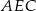 .
.
Podstawy trapezu równoramiennego o polu 40 mają długości 6 i 14. Oblicz długość ramienia tego trapezu.
Wykaż, że reszta z dzielenia sumy kwadratów czterech kolejnych liczb naturalnych przez 4 jest równa 2.
Oblicz sumę siedmiu początkowych wyrazów ciągu geometrycznego 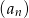 , w którym
, w którym 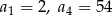 .
.
Wyznacz najmniejszą i największą wartość funkcji 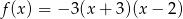 w przedziale
w przedziale 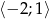 .
.
Ile jest możliwych kodów czterocyfrowych utworzonych z cyfr 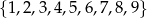 , w których są dokładnie dwie cyfry parzyste i dwie cyfry nieparzyste.
, w których są dokładnie dwie cyfry parzyste i dwie cyfry nieparzyste.
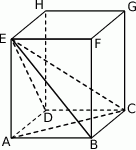
W graniastosłupie prawidłowym czworokątnym 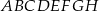 przekątna
przekątna 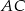 podstawy ma długość 4. Kąt
podstawy ma długość 4. Kąt 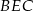 jest równy
jest równy 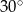 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 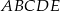 przedstawionego na poniższym rysunku.
przedstawionego na poniższym rysunku.
W pierwszym etapie konkursu matematycznego startowało 100 uczniów. Po pierwszym etapie z konkursu odpadło 50% dziewczynek oraz 15 chłopców. W drugim etapie konkursu wzięło udział trzy razy więcej chłopców niż dziewcząt. Ilu chłopców i ile dziewcząt wzięło udział w drugim etapie konkursu?

