/Szkoła średnia/Zadania maturalne
Dowody w geometrii twierdzenie Pitagorasa poziom rozszerzony
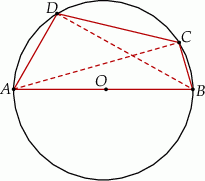
Bok 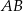 czworokąta
czworokąta 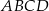 wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że
wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że 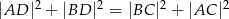 .
.
Wysokości w pewnym trójkącie 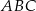 mają długości:
mają długości: 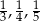 . Wykaż, że jest to trójkąt prostokątny.
. Wykaż, że jest to trójkąt prostokątny.
Wykaż, że jeżeli długości boków 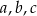 trójkąta prostokątnego są liczbami całkowitymi, to liczba
trójkąta prostokątnego są liczbami całkowitymi, to liczba 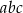 jest parzysta.
jest parzysta.
W trójkącie prostokątnym 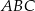 , w którym kąt przy wierzchołku
, w którym kąt przy wierzchołku 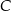 jest kątem prostym, poprowadzono środkowe
jest kątem prostym, poprowadzono środkowe 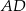 i
i 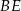 . Udowodnij, że
. Udowodnij, że 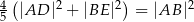 .
.
W pierścieniu kołowym cięciwa zewnętrznego okręgu ma długość 10 i jest styczna do wewnętrznego okręgu (zobacz rysunek).
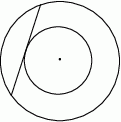
Wykaż, że pole tego pierścienia można wyrazić wzorem, w którym nie występują promienie wyznaczających go okręgów.
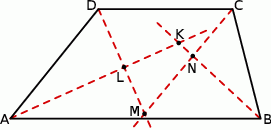
Dwusieczne kątów wewnętrznych trapezu 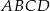 przecinają się w punktach
przecinają się w punktach 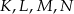 (patrz rysunek). Wykaż, że
(patrz rysunek). Wykaż, że 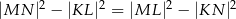 .
.
Czworokąt 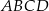 jest trapezem prostokątnym, w którym
jest trapezem prostokątnym, w którym 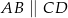 . Wykaż że
. Wykaż że
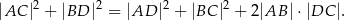
Przekątne czworokąta 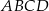 są prostopadłe. Wykaż, że
są prostopadłe. Wykaż, że 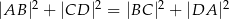 .
.
W trójkącie 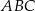 środkowe
środkowe 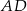 i
i 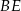 są prostopadłe. Wykaż, że
są prostopadłe. Wykaż, że 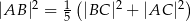 .
.
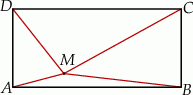
Punkt 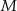 leży wewnątrz prostokąta
leży wewnątrz prostokąta 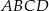 (zob. rysunek). Udowodnij, że
(zob. rysunek). Udowodnij, że 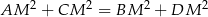 .
.
Punkt 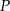 należy do okręgu opisanego na kwadracie
należy do okręgu opisanego na kwadracie 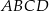 . Wykaż, że wyrażenie
. Wykaż, że wyrażenie 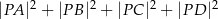 ma stałą wartość, niezależną od wyboru punktu
ma stałą wartość, niezależną od wyboru punktu 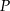 .
.
Dany jest prostokąt o polu 12, w którym długość przekątnej jest liczbą z przedziału 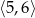 . Wykaż, że obwód tego prostokąta jest liczbą z przedziału
. Wykaż, że obwód tego prostokąta jest liczbą z przedziału 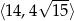 .
.
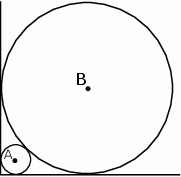
Dwa okręgi o środkach 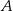 i
i 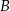 są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek pola większego z tych okręgów do pola mniejszego jest równy
są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek pola większego z tych okręgów do pola mniejszego jest równy 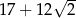 .
.